
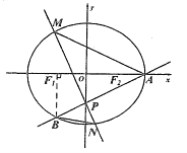
【题目】如图,椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,左、右焦点分别为
,左、右焦点分别为 ![]() ,过点
,过点 ![]() 且斜率为
且斜率为 ![]() 的直线与
的直线与 ![]() 轴交于点
轴交于点 ![]() ,与椭圆交于另一个点
,与椭圆交于另一个点 ![]() ,且点
,且点 ![]() 在
在 ![]() 轴上的射影恰好为点
轴上的射影恰好为点 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过点 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 两点(
两点( ![]() 不与
不与 ![]() 重合),若
重合),若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
【答案】
(1)解:当 ![]() 时,
时, ![]() 轴,得到点
轴,得到点 ![]()
所以
![]()
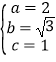 ,所以椭圆
,所以椭圆 ![]() 的方程是
的方程是 ![]()
(2)解:因为 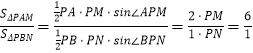 ,
, ![]() 所以
所以 ![]() .
.
设 ![]() ,则
,则 ![]() ,有
,有 ![]()
①当 ![]() 斜率不存在,
斜率不存在, ![]() 的方程为
的方程为 ![]() ,
,![]() 或
或 ![]() ,(不合条件,舍去)
,(不合条件,舍去)
②当 ![]() 斜率存在,由(Ⅰ)可知
斜率存在,由(Ⅰ)可知 ![]() ,设
,设 ![]() 方程为
方程为 ![]() ,
,
联立方程 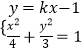 得:
得: ![]() .
.
由韦达定理可得 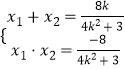 ,将
,将 ![]() 代入可得
代入可得 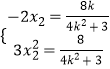 ,
,
即 ![]() .所以
.所以 ![]() .
.
所以直线 ![]() 的方程为
的方程为 ![]() 或
或 ![]()
【解析】(1)首先由条件得到直线AP的方程,根据“B和F1”的横坐标相同可得到B的坐标,代入直线AP,得到a,b,c一组关系;再由椭圆的性质a2=b2+c2得到一组关系;最后根据A点坐标,得到a=2,代入方程求解b,c的值。
(2)由上题已知A,B的坐标,面积之比为6,可以利用三角函数表示三角形的面积,将面积比转化为边长比,再转化为向量比,向量由点的坐标表示,可设出M,N的坐标和直线MN的方程;联立直线MN和椭圆,得到系数由k表示的一元二次方程,根据韦达定理得到x1和x2的关系,进而得到直线MN的斜率k。


科目:高中数学 来源: 题型:
【题目】在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,则λ的取值范围是( )
,则λ的取值范围是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间 ![]() 内单调递增;
内单调递增;
②函数y=f(x)在区间 ![]() 内单调递减;
内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x= ![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是( )
A.①②
B.②③
C.③④⑤
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式4ax-1<3x-4(a>0,且a≠1)对于任意的x>2恒成立,则a的取值范围为( )
A.![]()
B.![]()
![]()
C.[2,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市初三毕业生参加中考要进行体育测试,某实验中学初三(8)班的一次体育测试成绩的茎叶图和频率分布直方图都受到不同程度的涂黑,但可见部分如图,据此解答如下问题.
(Ⅰ)求全班人数及中位数,并重新画出频率直方图;
(Ⅱ)若要从分数在 ![]() 之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在
之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在 ![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com