
【题目】若关于x的不等式4ax-1<3x-4(a>0,且a≠1)对于任意的x>2恒成立,则a的取值范围为( )
A.![]()
B.![]()
![]()
C.[2,+∞)
D.(2,+∞)
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() :
: ![]() 的焦点为
的焦点为 ![]() ,过点
,过点 ![]() 分别作两条直线
分别作两条直线 ![]() ,
, ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 、
、 ![]() 两点,直线
两点,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 、
、 ![]() 两点,若
两点,若 ![]() 与
与 ![]() 的斜率的平方和为1,则
的斜率的平方和为1,则 ![]() 的最小值为( )
的最小值为( )
A.16
B.20
C.24
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点G是△ABO的重心. 
(1)求 ![]() +
+ ![]() +
+ ![]() ;
;
(2)若PQ过△ABO的重心G,且 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求证:
,求证: ![]() +
+ ![]() =3.
=3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2-mln x,g(x)=x2-(m+1)x.
x2-mln x,g(x)=x2-(m+1)x.
(1)求函数f(x)的单调区间;
(2)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
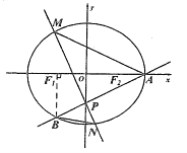
【题目】如图,椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,左、右焦点分别为
,左、右焦点分别为 ![]() ,过点
,过点 ![]() 且斜率为
且斜率为 ![]() 的直线与
的直线与 ![]() 轴交于点
轴交于点 ![]() ,与椭圆交于另一个点
,与椭圆交于另一个点 ![]() ,且点
,且点 ![]() 在
在 ![]() 轴上的射影恰好为点
轴上的射影恰好为点 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过点 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 两点(
两点( ![]() 不与
不与 ![]() 重合),若
重合),若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.存在 ![]() ,使得
,使得 ![]() 的否定是:不存在
的否定是:不存在 ![]() ,使得
,使得 ![]()
B.对任意 ![]() ,均有
,均有 ![]() 的否定是:存在
的否定是:存在 ![]() ,使得
,使得 ![]()
C.若 ![]() ,则
,则 ![]() 或
或 ![]() 的否命题是:若
的否命题是:若 ![]() ,则
,则 ![]() 或
或 ![]()
D.若 ![]() 为假命题,则命题
为假命题,则命题 ![]() 与
与 ![]() 必一真一假
必一真一假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中, ![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中的真命题是( )
是两个不同的平面,则下列命题中的真命题是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() 则
则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在 ![]() 上的函数
上的函数 ![]() 满足
满足 ![]() ,且
,且 ![]() 是偶函数,当
是偶函数,当 ![]() 时,
时, ![]() .令
.令 ![]() ,若在区间
,若在区间 ![]() 内,函数
内,函数 ![]() 有4个不相等实根,则实数
有4个不相等实根,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照 ![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费 ![]() (元)与月份
(元)与月份 ![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是 ![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com