
【题目】如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间 ![]() 内单调递增;
内单调递增;
②函数y=f(x)在区间 ![]() 内单调递减;
内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x= ![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是( )
A.①②
B.②③
C.③④⑤
D.③
【答案】D
【解析】对于①,函数y=f(x)在区间(﹣3,﹣ ![]() )内有增有减,故①不正确;
)内有增有减,故①不正确;
对于②,函数y=f(x)在区间(﹣ ![]() ,3)有增有减,故②不正确;
,3)有增有减,故②不正确;
对于③,函数y=f(x)当x∈(4,5)时,恒有f′(x)>0.故③正确;
对于④,当x=2时,函数y=f(x)有极大值,故④不正确;
对于⑤,当x=﹣ ![]() 时,f′(x)≠0,故⑤不正确.
时,f′(x)≠0,故⑤不正确.
故答案为:D.
利用使f′(x)>0的区间是增区间,使f′(x)<0的区间是减区间,分别对①②③进行逐一判定,导数等于零的值是极值,先增后减是极大值,先减后增是极小值,再对④⑤进行判定.导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() ﹣
﹣ ![]() (x为实常数).
(x为实常数).
(1)当a=1时,求函数φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;
(2)若方程e2f(x)=g(x)(其中e=2.71828…)在区间[ ![]() ]上有解,求实数a的取值范围.
]上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点G是△ABO的重心. 
(1)求 ![]() +
+ ![]() +
+ ![]() ;
;
(2)若PQ过△ABO的重心G,且 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求证:
,求证: ![]() +
+ ![]() =3.
=3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2-mln x,g(x)=x2-(m+1)x.
x2-mln x,g(x)=x2-(m+1)x.
(1)求函数f(x)的单调区间;
(2)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
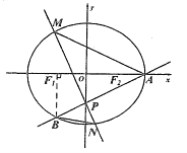
【题目】如图,椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,左、右焦点分别为
,左、右焦点分别为 ![]() ,过点
,过点 ![]() 且斜率为
且斜率为 ![]() 的直线与
的直线与 ![]() 轴交于点
轴交于点 ![]() ,与椭圆交于另一个点
,与椭圆交于另一个点 ![]() ,且点
,且点 ![]() 在
在 ![]() 轴上的射影恰好为点
轴上的射影恰好为点 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过点 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 两点(
两点( ![]() 不与
不与 ![]() 重合),若
重合),若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中, ![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中的真命题是( )
是两个不同的平面,则下列命题中的真命题是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() 则
则 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com