
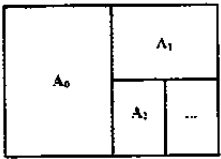
 An(n∈N)系列的纸张规格如图,其特色在于:
An(n∈N)系列的纸张规格如图,其特色在于:分析 由题意可得面积是逐渐变为上一个的一半,由相似可得x:y=$\sqrt{2}$:1,由此能求出这(n+1)张纸的重量之和Sn+1.
解答 解:由题意可得面积是逐渐变为上一个的一半,设An的长、宽分别为x,y,则An+1的长、宽分别为y,$\frac{1}{2}$x,
由相似可得x:y=$\sqrt{2}$:1,
故A4的面积为$\sqrt{2}$a2,A1的面积为8$\sqrt{2}$a2,A0的面积为16$\sqrt{2}{a}^{2}$,
所以Sn+1=$\frac{8\sqrt{2}{a}^{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}•b$+16$\sqrt{2}{a}^{2}b$
=16$\sqrt{2}$a2b(2-$\frac{1}{{2}^{n}}$)
=$32\sqrt{2}{a^2}b[{1-{{(\frac{1}{2})}^{n+1}}}]$.
故答案为:$32\sqrt{2}{a^2}b[{1-{{(\frac{1}{2})}^{n+1}}}]$.
点评 本题考查等比数列的求和,归纳推理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(a)>f(b) | B. | f(a)<f(b) | ||
| C. | f(a)=f(b) | D. | f(a)与f(b)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
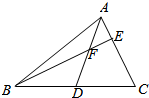 △ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:
△ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com