
分析 通过直接代入计算可知a2015=a4×504-1=-1,通过a2n=2an可知${a}_{{2}^{n-1}}$=2n-1、${a}_{3•{2}^{n-1}}$=-2n-1,进而可知前2015项中数值最大项为${a}_{{2}^{10}}$、最小项为${a}_{3•{2}^{9}}$,代入计算即可.
解答 解:依题意,a2015=a4×504-1=-1,
∵a4n-3=1,a4n-1=-1,a2n=2an,
∴a1=1,a3=-1,a2=2a1=2,a4=2a2=4,
∴${a}_{{2}^{n-1}}$=2n-1,
令2n-1<2015,则n最大为11,
∴前2015项中数值最大项为${a}_{{2}^{10}}$=a1024=1024,
同理${a}_{3•{2}^{n-1}}$=-2n-1,
令3•2n-1<2015,则n最大为10,
∴前2015项中数值最小项为${a}_{3•{2}^{9}}$=a1536=-29=-512,
∴前2015项中数值最大项与最小项的和为a1024+a1024=1024-512=512,
故答案为:-1、512.
点评 本题考查数列的通项,找出规律是解决本题的关键,注意解题方法的积累,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
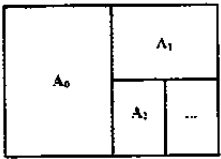 An(n∈N)系列的纸张规格如图,其特色在于:
An(n∈N)系列的纸张规格如图,其特色在于:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | [2,+∞) | C. | (1,$\sqrt{3}$] | D. | [$\sqrt{3},+∞$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com