
分析 (1)①求出θ∈(0,$\frac{π}{4}$]时f(θ)的解析式;
②求出θ∈($\frac{π}{4}$,$\frac{π}{2}$)时f(θ)的解析式,
利用分段函数写出f(θ)在(0,$\frac{π}{2}$)上的解析式;
(2)利用导数研究函数f(θ)在(0,$\frac{π}{2}$)上的单调性并求出最大值.
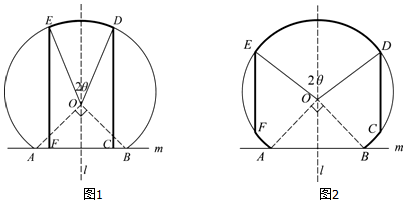
解答 解:(1)①当θ∈(0,$\frac{π}{4}$]时,ED=2θ,EF=$\frac{\sqrt{2}}{2}$+cosθ;
∴f(θ)=2aθ+2a($\sqrt{2}$+2cosθ);
②当θ∈($\frac{π}{4}$,$\frac{π}{2}$)时,ED+FA+BC=4θ-$\frac{π}{2}$,EF=2cosθ;
∴f(θ)=(4θ-$\frac{π}{2}$)a+2a(4cosθ);
由①②可得,f(θ)=$\left\{\begin{array}{l}{2a(θ+\sqrt{2}+2cosθ),θ∈(0,\frac{π}{4}]}\\{a(4θ-\frac{π}{4}+8cosθ),θ∈(\frac{π}{4},\frac{π}{2})}\end{array}\right.$;
(2)①当θ∈(0,$\frac{π}{4}$]时,f′(θ)=2a(1-2sinθ);
由a>0,填表如下:
| θ | (0,$\frac{π}{6}$] | $\frac{π}{6}$ | ($\frac{π}{6}$,$\frac{π}{4}$) |
| f′(θ) | + | 0 | - |
| f(θ) | 单调递增 | 极大值 | 单调递减 |
点评 本题考查了三角函数模型的应用问题,也考查了用导数研究函数的单调性与最值问题,是难题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${d_n}=\frac{{{c_1}+{c_2}+…+{c_n}}}{n}$ | B. | ${d_n}=\frac{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}{n}$ | ||
| C. | ${d_n}=\root{n}{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}$ | D. | ${d_n}=\root{n}{{\frac{{{c_1}^n•{c_2}^n{•_{\;}}{…_{\;}}•{c_n}^n}}{n}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [1,+∞) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com