
分析 写出原命题的否定,可判断①②;
构造函数f(x)=x2-2x并求出x∈[-1,2]时的最大值,可判断③;
举出正例x0=0,可判断④.
解答 解:①命题“对任意x∈R,有x2≥0”的否定是“存在x0∈R,有x02<0”,故错误;
②“存在x0∈R,使得x02-x0>0”的否定是:“任意x∈R,均有x2-x≤0”,故错误;
③f(x)=x2-2x的图象开口朝上,且以x=1为对称轴,对任意x∈[-1,2],x2-2x≤f(-1)=3,故正确;
④当x0=0时,x02+$\frac{1}{x_{0}^{2}+1}$=1,故存在x0∈R,使得x02+$\frac{1}{x_{0}^{2}+1}$≤1,故正确.
故真命题的序号为:③④,
故答案为:③④.
点评 本题以命题的真假判断与应用为载体,考查了全称命题,特称命题,二次函数的图象和性质,属于基础题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
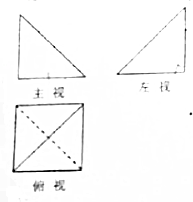 已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-3)、5 | B. | (-2,3)、5 | C. | (-2,3)、$\sqrt{5}$ | D. | ( 3,-2)、$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(sinα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
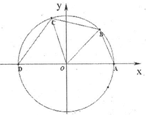 如图所示,已知点A(1,0),D(-1,0),点B,C在单位圆O上,且∠BOC=$\frac{π}{3}$.
如图所示,已知点A(1,0),D(-1,0),点B,C在单位圆O上,且∠BOC=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
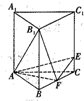 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{27}{14}$ | D. | -$\frac{23}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>2} | B. | {x|x>3或x<2} | C. | {x|2≤x≤3} | D. | {x|2<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com