
小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为x;小李后掷一枚骰子,向上的点数记为y,
(1)在直角坐标系xOy中,以(x,y)为坐标的点共有几个?试求点(x,y)落在直线x+y=7上的概率.
(2)规定:若x+y≥10,则小王赢;若x+y≤4,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
(1)因x,y都可取1,2,3,4,5,6,故以(x,y)为坐标的点共有36个.
记点(x,y)落在直线x+y=7上为事件A,事件A包含的点有:(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)6个,所以事件A的概率P(A)=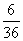 =
=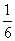 .
.
(2)记x+y≥10为事件B,x+y≤4为事件C,用数对(x,y)表示x,y的取值.则事件B包含(4,6),(5,5),(5,6),(6,4),(6,5),(6,6)共6个数对;
事件C包含(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)共6个数对.
由(1)知基本事件总数为36个,所以P(B)=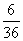 =
=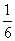 ,P(C)=
,P(C)=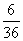 =
=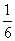 ,
,
所以小王、小李获胜的可能性相等,游戏规则是公平的.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
已知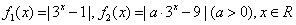 ,且
,且
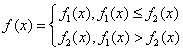
(1)当a=1时,求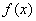 的解析式;
的解析式;
(2)在(1)的条件下,若方程 有4个不等的实根,求实数
有4个不等的实根,求实数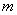 的范围;
的范围;
(3)当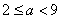 时,设
时,设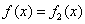 所对应的自变量取值区间的长度为l(闭区间[m,n]的长度定义为
所对应的自变量取值区间的长度为l(闭区间[m,n]的长度定义为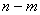 ),试求l的最大值.
),试求l的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
猎人在相距100 m处射击一野兔,命中的概率为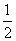 ,如果第一次未击中,则猎人进行第二次射击,但距离已是150 m,如果又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
,如果第一次未击中,则猎人进行第二次射击,但距离已是150 m,如果又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋子中有大小相同的四个小球,分别涂以红、白、黑、黄颜色.
(1)从中任取1球,取出白球的概率为________.
(2)从中任取2球,取出的是红球、白球的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋子中有四个小球,分别写有“神”、“十”、“飞”、“天”四个字,有放回地从中任取一个小球,取到“飞”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1、2、3、4表示取出小球上分别写有“神”、“十”、“飞”、“天”四个字,以每两个随机数为一组,代表两次的结果.经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止概率为( )
A.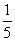 B.
B.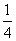
C.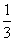 D.
D.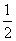
查看答案和解析>>
科目:高中数学 来源: 题型:
把[0,1]内的均匀随机数分别转化为[0,4]和[-4,1]内的均匀随机数,需实施的变换分别为( )
A.y=-4x,y=5-4 B.y=4x-4,y=4x+3
C.y=4x,y=5x-4 D.y=4x,y=4x+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com