练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

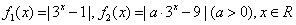    已知，且

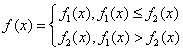
    （1）当a=1时，求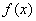的解析式；

    （2）在（1）的条件下，若方程有4个不等的实根，求实数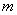的范围；

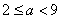    （3）当时，设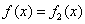 所对应的自变量取值区间的长度为l（闭区间[m,n]的长度定义为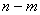），试求l的最大值.


    解: (1)当时,.

    故  

    易知当时

    所以-------------------------------------3                        

    （2），可画出和的图像，

    由数形结合可知，当时方程有4个不等的实根 -----6

    （3）当时,因为,,

    所以由,解得,

    从而当时,

    当时,因为,,

    所以由,解得,

    从而当时,

    当时,因为,

    从而 一定不成立

    综上得,当且仅当时,,      

    故

    从而当时,取得最大值为  

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某单位为了解用电量y(度)与气温x(℃)之间的关系，随机抽查了某4天的用电量与当天气温，并制作了对照表：

    气温(℃)

    18

    13

    10

    －1

    用电量(度)

    24

    34

    38

    64

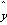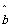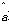    由表中数据得线性回归方程＝x＋中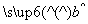＝－2，预测当气温为－4℃时，用电量约为________度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二项式的展开式中含的项的系数是                ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    f(x)，g(x)分别是R上的奇函数、偶函数，且f(x)－g(x)＝ex，则有(　　)

    A．f(2)<f(3)<g(0)                      B．g(0)<f(3)<f(2)

    C．f(2)<g(0)<f(3)                      D．g(0)<f(2)<f(3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{x|≤2x＋1≤16}，B＝{x|m＋1≤x≤3m－1}．

        (1)求集合A；

    (2)若B⊆A，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的定义域为，则函数的定义域为               (      )

    A．　　  　 B．　　　C． 　　　D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数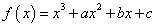，在定义域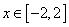上表示的曲线过原点，且在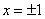处的切线斜率均为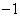.有以下命题：

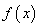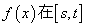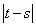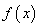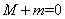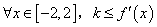    ①是奇函数；②若内递减，则的最大值为4；③的最大值为M，最小值为m，则；④若对恒成立，则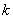的最大值为2.其中正确命题的个数为                                               （      ）

    A.     1个               B.2个                  C.3个             D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知随机事件A发生的频率是0.02，事件A出现了10次，那么共进行了________次试验．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    小王、小李两位同学玩掷骰子(骰子质地均匀)游戏，规则：小王先掷一枚骰子，向上的点数记为x；小李后掷一枚骰子，向上的点数记为y，

    (1)在直角坐标系xOy中，以(x，y)为坐标的点共有几个？试求点(x，y)落在直线x＋y＝7上的概率．

    (2)规定：若x＋y≥10，则小王赢；若x＋y≤4，则小李赢，其他情况不分输赢．试问这个游戏规则公平吗？请说明理由．

    查看答案和解析>>

    同步练习册答案