
【题目】已知数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,
, ![]() .
.
(Ⅰ)求 ![]() ,猜想
,猜想 ![]() 的通项公式,并用数学归纳法证明;
的通项公式,并用数学归纳法证明;
(Ⅱ)设 ![]() ,求证:数列
,求证:数列 ![]() 中任意三项均不成等比数列.
中任意三项均不成等比数列.
【答案】解:(Ⅰ)求出 ![]() ,猜想
,猜想 ![]() ,数学归纳法证明:
,数学归纳法证明:
(ⅰ)当 ![]() 时,猜想成立;
时,猜想成立;
(ⅱ)假设当 ![]() 时,猜想成立,即
时,猜想成立,即 ![]()
当 ![]() 时,
时, ![]()
∴当 ![]() 时,猜想也成立
时,猜想也成立
综上,对一切 ![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)得 ![]() .
.
假设数列 ![]() 中存在三项
中存在三项 ![]() (
( ![]() 互不相等)成等比数列,
互不相等)成等比数列,
则 ![]() .即
.即 ![]() .
.
∴ ![]() ∵
∵ ![]() ,
,
∴ ![]() ∴
∴ ![]() ,
, ![]() ,∴
,∴ ![]() .
.
与 ![]() 矛盾.
矛盾.
所以数列 ![]() 中任意不同的三项都不可能成等比数列
中任意不同的三项都不可能成等比数列
【解析】(1)先由已知归纳猜想出一般结论,再用数学归纳法证明。
(2)证明数列是等比数列或不是等比数列,都得紧扣定义,这里用反证法。
【考点精析】解答此题的关键在于理解等比数列的定义的相关知识,掌握如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“x1x2∈(0,+∞)且x1≠x2有(x1﹣x2)[f(x1)﹣f(x2)]<0”的是( )
A.f(x)= ![]() ﹣x
﹣x
B.f(x)=x3
C.f(x)=lnx+ex
D.f(x)=﹣x2+2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() 是棱
是棱 ![]() 的中点,且
的中点,且 ![]() .
.
(1)试在棱 ![]() 上确定一点
上确定一点 ![]() ,使
,使 ![]() 平面
平面 ![]() ;
;
(2)当点 ![]() 在棱
在棱 ![]() 中点时,求直线
中点时,求直线 ![]() 与平面
与平面 ![]() 所成角的大小的正弦值。
所成角的大小的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将红、黑、蓝、白5张纸牌(其中白纸牌有2张)随机分发给甲、乙、丙、丁4个人,每人至少分得1张,则下列两个事件为互斥事件的是( )
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜奶店每天以每瓶3元的价格从牧场购进若干瓶鲜牛奶,然后以每瓶7元的价格出售.如果当天卖不完,剩下的鲜牛奶作垃圾处理.
(1)若鲜奶店一天购进30瓶鲜牛奶,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:瓶,
(单位:瓶,![]() )的函数解析式;
)的函数解析式;
(2)鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶),绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5);

(i)若该鲜奶店一天购进30瓶鲜牛奶,求这100天的日利润(单位:元)的平均数;
(ii) 若该鲜奶店一天购进30瓶鲜牛奶,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为定义域
是否为定义域![]() 上的“局部奇函数”?若是,求出所有满足
上的“局部奇函数”?若是,求出所有满足![]() 的
的![]() 的值;若不是,请说明事由.
的值;若不是,请说明事由.
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
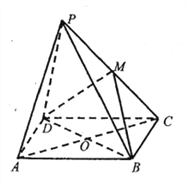
【题目】如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 的所成角的大小.
的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() +
+ ![]() +
+ ![]() ≥3.
≥3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com