
分析 (1)由已知直接利用组合公式能求出7${C}_{6}^{3}-4{C}_{7}^{4}$的值.
(2)对任意m∈N*,当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C${\;}_{m}^{m}$+(m+2)C${\;}_{m+1}^{m}$+(m+3)C${\;}_{m+2}^{m}$+…+nC${\;}_{n-1}^{m}$+(n+1)C${\;}_{n}^{m}$=(m+1)C${\;}_{n+2}^{m+2}$.
解答 解:(1)7${C}_{6}^{3}-4{C}_{7}^{4}$
=$7×\frac{6×5×4}{3×2×1}$-4×$\frac{7×6×5×4}{4×3×2×1}$
=7×20-4×35=0.
证明:(2)对任意m∈N*,
①当n=m时,左边=(m+1)${C}_{m}^{m}$=m+1,
右边=(m+1)${C}_{m+2}^{m+2}$=m+1,等式成立.
②假设n=k(k≥m)时命题成立,
即(m+1)C${\;}_{m}^{m}$+(m+2)C${\;}_{m+1}^{m}$+(m+3)C${\;}_{m+2}^{m}$+…+k${C}_{k-1}^{m}$+(k+1)${C}_{k}^{m}$=(m+1)${C}_{k+2}^{m+2}$,
当n=k+1时,
左边=(m+1)${C}_{m}^{m}$+(m+2)${C}_{m+1}^{m}$+(m+3)${C}_{m+2}^{m}$+$…+k{C}_{k-1}^{m}$+(k+1)${C}_{k}^{m}$+(k+2)${C}_{k+1}^{m}$
=$(m+1){C}_{k+2}^{m+2}+(k+2){C}_{k+1}^{m}$,
右边=$(m+1){C}_{k+3}^{m+2}$
∵$(m+1){C}_{k+3}^{m+2}-(m+1){C}_{k+2}^{m+2}$
=(m+1)[$\frac{(k+3)!}{(m+2)!(k-m+1)!}$-$\frac{(k+2)!}{(m+2)!(k-m)!}$]
=(m+1)×$\frac{(k+2)!}{(m+2)!(k-m+1)!}$[k+3-(k-m+1)]
=(k+2)$\frac{(k+1)!}{m!(k-m+1)!}$
=(k+2)${C}_{k+1}^{m}$,
∴$(m+1){C}_{k+2}^{m+2}+(k+2){C}_{k+1}^{m}$=(m+1)${C}_{k+3}^{m+2}$,
∴左边=右边,
∴n=k+1时,命题也成立,
∴m,n∈N*,n≥m,(m+1)C${\;}_{m}^{m}$+(m+2)C${\;}_{m+1}^{m}$+(m+3)C${\;}_{m+2}^{m}$+…+nC${\;}_{n-1}^{m}$+(n+1)C${\;}_{n}^{m}$=(m+1)C${\;}_{n+2}^{m+2}$.
点评 本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和数学归纳法的合理运用.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
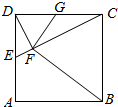 如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向上平行移动$\frac{π}{3}$个单位长度 | D. | 向下平行移动$\frac{π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com