练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知集合P={x?x-1≤0}，Q={x?0＜x≤2}，则（CRP）∩Q=（　　）
    A．（0，1）B．（0.2]C．[1，2]D．（1，2]

    分析 求得P的补集，再由交集的定义，即可得到所求集合．

    解答 解：集合P={x?x-1≤0}={x|x≤1}，
    CRP={x|x＞1}，
    Q={x?0＜x≤2}，
    则（CRP）∩Q={x|1＜x≤2}．
    故选：D．

    点评 本题考查集合的运算：交集和补集，考查运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）-cos（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为$\frac{π}{2}$．
    （1）求$f（\frac{7π}{8}）$的值；
    （2）求函数g（x）=f（x）+f（x+$\frac{π}{4}$）的对称轴与单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某风景区水面游览中心计划国庆节当日投入之多3艘游船供游客观光，过去10年的数据资料显示每年国庆节当日客流量X（单位：万人）都大于1，并把客流量分成三段整理得下表：
    国庆节当日客流量X1＜X＜33≤X≤5X＞5
    频数244
    以这10年的数据资料记录的隔断客流量的频率作为每年客流量在隔断发生的概率，且每年国庆节当日客流量相互独立．
    （1）求未来连续3年国庆节当日中，恰好有1年国庆节当日客流量超过5万人的概率；
    （2）该水面游览中心希望投入的游船尽可能使用，但每年国庆节当日游船最多使用量：（单位：艘）受当日客流量X（单位：万人）的限制，其关联关系如下表：
    国庆节当日客流量X1＜X＜33≤X≤5X＞5
    游船最多使用量123
    若某艘游船国庆节当日使用，则水面游览中心国庆节当日可获得利润3万元，若某艘游船国庆节当日不使用，则水面游览中心国庆节当日亏损0.5万元，记Y（单位：万元）表示该水面游览中心国庆节当日获得总利润，当Y的数学期望最大时称水面游览中心在国庆节当日效益最佳，问该水面游览中心的国庆节当日应投入多少艘游船才能使该水面游览中心在国庆节当日效益最佳？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

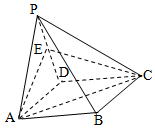    6．在四棱锥P-ABCD中，平面PAD⊥平面ABCD，∠APD=90°，PA=PD=AB=a，ABCD是矩形，E是PD的中点．
    （1）求证：PB⊥AC．
    （2）求二面角E-AC-D的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在数列{an}中，a1=1an+1=$\frac{2（n+1）}{n}{a_n}$，n∈N*．
    （1）求证数列$\left\{{\frac{a_n}{n}}\right\}$为等比数列．
    （2）求数列{an}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．“a＞1”是“函数f（x）=ax-sinx在R上是增函数”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知三棱锥S-ABC的各项顶点都在一个表面积为4π的球表面上，球心O在AB上，SO⊥平面ABC，AC=$\sqrt{2}$，则三棱锥S-ABC的表面积为2+$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

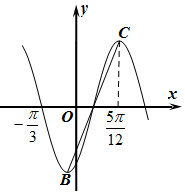    7．若函数f（x）=Asin（ωx+φ）（A）＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$的部分图象如图所示，B，C分别是图象的最低点和最高点，
    其中|BC|=$\sqrt{\frac{{π}^{2}}{4}+16}$．
    （I）求函数f（x）的解析式；
    （II）在锐角△ABC中，a，b，c分别是角A、B、C的对边，若f（A）=$\sqrt{3}$，a=2，求△ABC周长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列不是随机变量的是（　　）
    A．从编号为1～10号的小球中随意取一个小球的编号
    B．从早晨7：00到中午12：00某人上班的时间
    C．A、B两地相距a km，以v km/h的速度从A到达B的时间
    D．某十字路口一天中经过的轿车辆数

    查看答案和解析>>

    同步练习册答案