
分析 (1)利用两角差的正弦函数公式化简函数解析式可得f(x)=2sin(ωx+φ-$\frac{π}{6}$),由f(x)是偶函数,可得φ=$\frac{2π}{3}$+kπ(k∈Z),结合范围0<φ<π,可求φ,利用周期公式可求ω,即可求得函数解析式为f(x)=2cos 2x.利用诱导公式,特殊角的三角函数值即可求值得解.
(2)利用三角函数恒等变换的应用可得解析式g(x)=2$\sqrt{2}$sin(2x+$\frac{3π}{4}$),令2x+$\frac{3π}{4}$=$\frac{π}{2}$+kπ,k∈Z,即可解得对称轴方程,令-$\frac{π}{2}$+2kπ≤2x+$\frac{3π}{4}$≤$\frac{π}{2}$+2kπ,即可解得单调递增区间,令$\frac{π}{2}$+2kπ≤2x+$\frac{3π}{4}$≤$\frac{3π}{2}$+2kπ,解得单调递减区间.
解答 解:(1)f(x)=$\sqrt{3}$sin(ωx+φ)-cos(ωx+φ)
=2[$\frac{\sqrt{3}}{2}$sin(ωx+φ)-$\frac{1}{2}$cos(ωx+φ)
=2sin(ωx+φ-$\frac{π}{6}$).
因为f(x)是偶函数,
则φ-$\frac{π}{6}$=$\frac{π}{2}$+kπ(k∈Z),
所以φ=$\frac{2π}{3}$+kπ(k∈Z),
又因为0<φ<π,
所以φ=$\frac{2π}{3}$,
所以f(x)=2sin($ωx+\frac{π}{2}$)=2cosωx.
由题意得$\frac{2π}{ω}$=2•$\frac{π}{2}$,
所以ω=2.
故f(x)=2cos 2x.
因此$f(\frac{7π}{8})$=2cos$\frac{7π}{4}$=$\sqrt{2}$.
(2)g(x)=2cos 2x+2cos 2(x+$\frac{π}{4}$)
=2cos 2x+2cos(2x+$\frac{π}{2}$)
=2cos 2x-2sin 2x
=2$\sqrt{2}$sin(2x+$\frac{3π}{4}$),
令2x+$\frac{3π}{4}$=$\frac{π}{2}$+kπ,k∈Z,解得对称轴x=-$\frac{π}{8}$+$\frac{1}{2}$kπ,k∈Z,
令-$\frac{π}{2}$+2kπ≤2x+$\frac{3π}{4}$≤$\frac{π}{2}$+2kπ,解得:-$\frac{5π}{8}$+kπ≤x≤-$\frac{π}{8}$+kπ,k∈Z,
令$\frac{π}{2}$+2kπ≤2x+$\frac{3π}{4}$≤$\frac{3π}{2}$+2kπ,解得:-$\frac{π}{8}$+kπ≤x≤$\frac{3π}{8}$+kπ,k∈Z,
所以函数g(x)的对称轴x=-$\frac{π}{8}$+$\frac{1}{2}$kπ,k∈Z,
单调递增区间为:[-$\frac{5π}{8}$+kπ,-$\frac{π}{8}$+kπ],k∈Z,单调递减区间为:[-$\frac{π}{8}$+kπ,$\frac{3π}{8}$+kπ],k∈Z.
点评 本题主要考查了三角函数恒等变换的应用及正弦函数的图象和性质的应用,考查了转化思想,属于基础题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
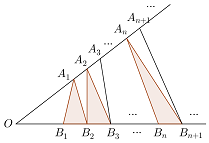 如图,点列{An}、{Bn}分别在锐角两边(不在锐角顶点),且|AnAn+1|=|An+1An+2|,An≠An+2,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1,n∈N*(P≠Q表示点P与Q不重合),若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )
如图,点列{An}、{Bn}分别在锐角两边(不在锐角顶点),且|AnAn+1|=|An+1An+2|,An≠An+2,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1,n∈N*(P≠Q表示点P与Q不重合),若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )| A. | {dn}是等差数列 | B. | {Sn}是等差数列 | ||
| C. | {d${\;}_{n}^{2}$}是等差数列 | D. | {S${\;}_{n}^{2}$}是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{π^2}+4}$ | B. | $2\sqrt{{π^2}+1}$ | C. | $\sqrt{\frac{π^2}{4}+4}$ | D. | $\sqrt{\frac{π^2}{16}+4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0.2] | C. | [1,2] | D. | (1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com