
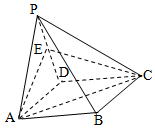
 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.分析 (1)设AD中点为F,连接BF、PF,推导出△ABC∽△FAB,从而AC⊥BF,推导出PF⊥AC,由此能证明AC⊥PB.
(2)过E作EH∥PF,EH交AD于H,过H作HO⊥AC,交AC于O,连接EO,则∠EOH为二面角E-AC-D的平面角,由此能求出二面角E-AC-D的正切值.
解答 证明:(1)设AD中点为F连接BF、PF.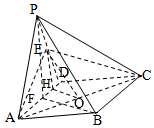
∵PA=PD=AB=a,∴$AD=BC=\sqrt{2}a,AF=\frac{{\sqrt{2}}}{2}a$,
∴$\frac{AB}{AF}=\frac{BC}{AB}=\sqrt{2}$.
∴△ABC∽△FAB,∴AC⊥BF,…(4分)
又∵PF⊥AD,又∵平面PAD⊥平面ABCD.
平面PAD∩平面ABCD=AD,
∴PF⊥面ABC,∴PF⊥AC,
∴AC⊥平面PBF,AC⊥PB.…(6分)
解:(2)过E作EH∥PF,EH交AD于H,
过H作HO⊥AC,交AC于O,连接EO.
由(1)知EH⊥面ACD,HO⊥AC,
∴∠EOH为二面角E-AC-D的平面角…(8分)
$EH=\frac{1}{2}PF=\frac{{\sqrt{2}}}{4}a$.
$OH=AHsin∠HAO=\frac{{3\sqrt{2}}}{4}a•\frac{{\sqrt{3}}}{3}=\frac{{\sqrt{6}}}{4}a$.
∴$tan∠EOH=\frac{EH}{OH}=\frac{{\sqrt{3}}}{3}$.
∴二面角E-AC-D的正切值为$\frac{\sqrt{3}}{3}$.…(12分)
点评 本题考查线线垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
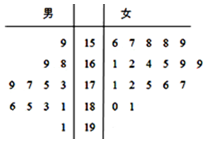 某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.
某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0.2] | C. | [1,2] | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(sinβ) | B. | f(sinα)<f(cosβ) | C. | f(cosα)<f(cosβ) | D. | f(sinα)>f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-2 | B. | y=x3 | C. | y=ln(x+$\sqrt{{x^2}+1}$) | D. | y=sin2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com