练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设各项都是正数的等比数列{an}，Sn为前n项和，且S10＝10，S30＝70，那么S40＝(　　)

    A．150                                   B．－200

    C．150或－200                      D．400或－50


    A　依题意，数列S10，S20－S10，S30－S20，S40－S30成等比数列，因此有(S20－S10)2＝S10(S30－S20)，即(S20－10)2＝10(70－S20)，故S20＝－20或S20＝30；又S20>0，

    因此S20＝30，S20－S10＝20，S30－S20＝40，故S40－S30＝80.S40＝150.选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知△ABC和点M满足＋＋＝0.若存在实数m使得＋＝m成立，则m＝________.　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知有限数列，，，，…，(m≥7，且m∈N*)．

    (1)指出这个数列的一个通项公式；

    (2)判断0.98是不是这个数列中的项？若是，是第几项？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知Sn是等差数列{an}的前n项和，S10>0并且S11＝0，若Sn≤Sk对n∈N*恒成立，则正整数k构成的集合为(　　)

    A．{5}                                   B．{6}

    C．{5,6}                                D．{7}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1＝1，an＋1＝r·an＋r(n∈N*，r∈R且r≠0)，则“r＝1”是“数列{an}为等差数列”的(　　)

    A．充分不必要条件                B．必要不充分条件

    C．充分必要条件                   D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且Sn＝4an－3(n∈N*)．

    (1)证明：数列{an}是等比数列；

    (2)若数列{bn}满足bn＋1＝an＋bn(n∈N*)，且b1＝2，求数列{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足an＋an＋1＝(n∈N*)，a1＝－，Sn是数列{an}的前n项和，则S2 013＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


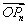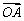    已知点A(1,0)，B(0,1)和互不相同的点P1，P2，P3，…，Pn，…，满足＝an＋bn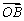 (n∈N*)，其中{an}，{bn}分别为等差数列和等比数列，O为坐标原点，若P1是线段AB的中点．

    (1)求a1，b1的值．

    (2)点P1，P2，P3，…，Pn，…能否在同一条直线上？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系

    中，点关于直线的对称点的极坐标为          .

    查看答案和解析>>

    同步练习册答案