
分析 (1)令f(x)=xt-1-t(x-1),x∈(0,1)时,xt-1≤1,f′(x)≤0,函数单调递减;x>1时,f′(x)>0,函数单调递增,得到x=1是f(x)的唯一极小值点,则f(x)≥f(1)=0,即可得证;
(2)分a=b和a≠b两种情况证明结论,并构造函数φ(x)=xa-xb,先证得φ(x)是单调减函数,进而得到结论.
解答 证明:(1)令f(x)=xt-1-t(x-1),f′(x)=t(xt-1-1),
∵t>1,∴t-1>0,
x∈(0,1)时,xt-1≤1,f′(x)≤0,函数单调递减;x>1时,f′(x)>0,函数单调递增,
∴x=1是f(x)的唯一极小值点,
∴f(x)≥f(1)=0,
即:xt≥1+t(x-1);
(2)当a=b,不等式显然成立;
当a≠b时,不妨设a<b,
则aa+bb≥ab+ba?aa-ab≥ba-bb,
令φ(x)=xa-xb,x∈[a,b]
下证φ(x)是单调减函数.
∵φ′(x)=axa-1-bxb-1=axb-1(xa-b-$\frac{b}{a}$)
易知a-b∈(-1,0),1+a-b∈(0,1),$\frac{1}{1+a-b}$>1,
由(1)知当t>1,(1+x)t>1+tx,x∈[a,b],
∴${b}^{\frac{1}{1+a-b}}$=$[1+(b-1)]^{\frac{1}{1+a-b}}$>1+$\frac{b-1}{1+a-b}$=$\frac{a}{1+a-b}$>a,
∴b>a1+a-b,∴$\frac{b}{a}$>aa-b≥xa-b,
∴φ'(x)<0,
∴φ(x)在[a,b]上单调递减.
∴φ(a)>φ(b),
即aa-ab>ba-bb,
∴aa+bb>ab+ba.
综上,aa+bb≥ab+ba成立.
点评 考查不等式的证明,考查运用导数判断函数的单调性,证明不等式的方法,构造函数是解题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (3,4) | C. | (-3,-4) | D. | (-3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
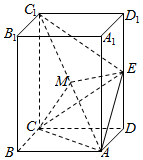 如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.
如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:已知⊙O是△ABC的外接圆,AB=BC,AH是BC边上的高,延长交⊙O于点D,AE是⊙O的直径.
如图:已知⊙O是△ABC的外接圆,AB=BC,AH是BC边上的高,延长交⊙O于点D,AE是⊙O的直径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com