
分析 (1)由对数函数的定义即可求出函数的定义域,
(2)根据偶函数的性质,即可求出a的值,
(3)解法一:根据函数零点定理可得关于t的方程组,解得即可,解法二:分别作出函数y=x2+x-1(-1<x<1)和y=2t的图象,由图象可得.
解答 解:(1)由$\left\{{\begin{array}{l}{1+x>0}\\{1-x>0}\end{array}}\right.$解得-1<x<1,所以函数f(x)的定义域为(-1,1).
(2)依题意,可知f(x)为偶函数,所以f(-x)=f(x),即log2(1-x)+alog2(1+x)=log2(1+x)+alog2(1-x),
即(a-1)[log2(1+x)-log2(1-x)]=0,即$(a-1){log_2}\frac{1+x}{1-x}=0$在(-1,1)上恒成立,所以a=1.
(3)解法一:由(2)可知$f(x)={log_2}(1+x)+{log_2}(1-x)={log_2}(1-{x^2})$,
所以g(x)=x2+x-1-2t,它的图象的对称轴为直线$x=-\frac{1}{2}$.
依题意,可知g(x)在(-1,1)内有两个不同的零点,
只需$\left\{{\begin{array}{l}{g(-1)=-1-2t>0}\\{g({-\frac{1}{2}})=-\frac{5}{4}-2t<0}\\{g(1)=1-2t>0}\end{array}}\right.$,解得$-\frac{5}{8}<t<-\frac{1}{2}$.
所以实数t的取值范围是$({-\frac{5}{8},-\frac{1}{2}})$.
解法二:由(2)可知$f(x)={log_2}(1+x)+{log_2}(1-x)={log_2}(1-{x^2})$,
所以g(x)=x2+x-1-2t.
依题意,可知g(x)在(-1,1)内有两个不同的零点,即方程2t=x2+x-1在(-1,1)内有两个不等实根,
即函数y=2t和y=x2+x-1在(-1,1)上的图象有两个不同的交点.
在同一坐标系中,分别作出函数y=x2+x-1(-1<x<1)和y=2t的图象,如图所示.
观察图形,可知当$-\frac{5}{4}<2t<-1$,即$-\frac{5}{8}<t<-\frac{1}{2}$时,两个图象有两个不同的交点.
所以实数t的取值范围是$({-\frac{5}{8},-\frac{1}{2}})$.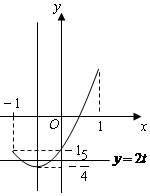
点评 本题以对数型函数为例,考查了函数的单调性和定义域,函数的奇偶性和函数零点定理,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
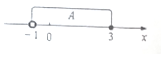
| A. | {-1,0,1,2,3} | B. | {0,1,2,3} | C. | {1,2,3} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2n | C. | 3n | D. | 4n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com