
【题目】在正方体![]() 中,棱长为2,
中,棱长为2,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 为底面正方形
为底面正方形![]() 内一点(含边界)且
内一点(含边界)且![]() 与面
与面![]() 所成角的正切值为
所成角的正切值为![]() ,直线
,直线![]() 与面
与面![]() 的交点为
的交点为![]() ,当
,当![]() 到
到![]() 的距离最小时,则四面体
的距离最小时,则四面体![]() 外接球的表面积为___________.
外接球的表面积为___________.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上一动点,动点
上一动点,动点![]() 满足
满足![]() .
.
(1)求![]() 点轨迹的直角坐标方程;
点轨迹的直角坐标方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 是
是![]() 上一个动点,求
上一个动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为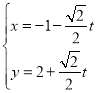 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为![]() ,曲线C2的直角坐标方程为
,曲线C2的直角坐标方程为![]() .
.
(1)若直线l与曲线C1交于M、N两点,求线段MN的长度;
(2)若直线l与x轴,y轴分别交于A、B两点,点P在曲线C2上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),an=an+b(n∈N*).
(1)求{an};
(2)设数列{an}的前n项和为Sn,bn![]() ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作平面
作平面![]() 的垂线,垂足为
的垂线,垂足为![]() 与
与![]() 的交点
的交点![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
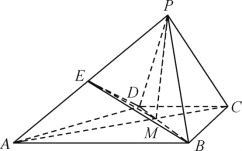
(1)求证:DE//平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为迎接“618年中庆典,拟推出促销活动,活动规则如下:①活动期间凡在商场内购物,每满673元可参与一次现金红包抽奖,且互不影响,详细如下表:
奖项 | 一等奖 | 二等奖 |
奖金 | 200元现金红包 | 优惠餐券1张(价值50元) |
获奖率 | 30% | 70% |
②活动期间凡在商场内购物,每满2019元可参与消费返现,返现金额为实际消费金额的15%.规定每位顾客只可选择参加其中一种优惠活动.
(1)现有顾客甲在商场消费2019元,若其选择参与抽奖,求其可以获得现金红包的概率.
(2)现有100名消费金额为2019元的顾客正在等待抽奖,假如你是该商场的活动策划人,你更希望顾客参与哪项优惠活动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数列![]() ,规定
,规定![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,规定
,规定![]() 为
为![]() 的二阶差分数列,其中
的二阶差分数列,其中![]() .
.
(1)数列![]() 的通项公式
的通项公式![]() ,试判断
,试判断![]() ,
,![]() 是否为等差数列,请说明理由?
是否为等差数列,请说明理由?
(2)数列![]() 是公比为
是公比为![]() 的正项等比数列,且
的正项等比数列,且![]() ,对于任意的
,对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求
,求![]() 所有可能的取值构成的集合;
所有可能的取值构成的集合;
(3)各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,对满足
,对满足![]() ,
,![]() 的任意正整数
的任意正整数![]() 、
、![]() 、
、![]() ,都有
,都有![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案![]() 是报废原有生产线,重建一条新的生产线;方案
是报废原有生产线,重建一条新的生产线;方案![]() 是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期平均年利润(单位:万元) | 方案 | 700 | 400 |
|
方案 | 600 | 300 |
| |
(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?
(2)记该生产线升级后的产品(以下简称“新产品”)的年产量为![]() (万件),通过核算,实行方案
(万件),通过核算,实行方案![]() 时新产品的年度总成本
时新产品的年度总成本![]() (万元)为
(万元)为![]() ,实行方案
,实行方案时新产品的年度总成本
![]() (万元)为
(万元)为![]() .已知
.已知![]() ,
,![]() .若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价
.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价![]() (元)分别为60,
(元)分别为60,![]() ,
,![]() ,且生产的新产品当年都能卖出去.试问:当
,且生产的新产品当年都能卖出去.试问:当![]() 取何值时,新产品年利润
取何值时,新产品年利润![]() 的期望取得最大值?并判断这一年利润能否达到预期目标.
的期望取得最大值?并判断这一年利润能否达到预期目标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 在对角线
在对角线![]() 上运动.当
上运动.当![]() 的面积取得最小值时,点
的面积取得最小值时,点![]() 的位置是( )
的位置是( )

A.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() B.线段
B.线段![]() 的中点
的中点
C.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() D.线段
D.线段![]() 的四等分点,且靠近点
的四等分点,且靠近点![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com