设等比数列{an}的前n项的和为Sn,且对任意n∈N*,Sn>0,则数列{an}的公比的取值范围为( )
A.(-∞,0)∪(1,+∞)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-1,0)∪(0,+∞)
【答案】
分析: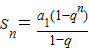
,由S
1=a
1>0,知
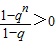
恒成立,当q>1时,q
n>1恒成立;当q=1时,只要a
1>0,S
n>0就一定成立.当q<1时,1-q
n>0必须恒成立;当0<q<1时,1-q
n>0恒成立;当-1<q<0时,1-q
n>0也恒成立;当q<-1时,当n为偶数时,1-q
n>0不成立;当q=-1时,显然1-q
n>0也不可能恒成立.由此能得到q的取值范围.
解答:解:
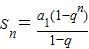
,
∵S
n>0,∴a
1>0,
则
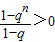
恒成立,
当q>1时,1-q
n<0恒成立,
即q
n>1恒成立,
又q>1,所以这显然成立,
当q=1时,只要a
1>0,S
n>0就一定成立.
当q<1时,
1-q
n>0必须恒成立
当0<q<1时,1-q
n>0恒成立
当-1<q<0时,1-q
n>0也恒成立
当q<-1时,当n为偶数时
1-q
n>0不成立
当q=-1时,显然1-q
n>0也不可能恒成立
所以q的取值范围为(-1,0)∪(0,+∞).
故选D.
点评:本题考查数列{a
n}的公比的取值范围的求法,解题时要认真审题,注意分类讨论思想的合理运用.

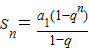 ,由S1=a1>0,知
,由S1=a1>0,知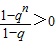 恒成立,当q>1时,qn>1恒成立;当q=1时,只要a1>0,Sn>0就一定成立.当q<1时,1-qn>0必须恒成立;当0<q<1时,1-qn>0恒成立;当-1<q<0时,1-qn>0也恒成立;当q<-1时,当n为偶数时,1-qn>0不成立;当q=-1时,显然1-qn>0也不可能恒成立.由此能得到q的取值范围.
恒成立,当q>1时,qn>1恒成立;当q=1时,只要a1>0,Sn>0就一定成立.当q<1时,1-qn>0必须恒成立;当0<q<1时,1-qn>0恒成立;当-1<q<0时,1-qn>0也恒成立;当q<-1时,当n为偶数时,1-qn>0不成立;当q=-1时,显然1-qn>0也不可能恒成立.由此能得到q的取值范围.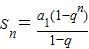 ,
,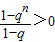 恒成立,
恒成立,

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案