
| A. | (-∞,0) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
分析 利用函数的零点与方程根的关系,通过函数的导数求解函数斜率,然后求解a的范围即可.
解答 解:关于x的方程$\frac{1}{x+2}=a|x|$有三个不同的实数解,
就是函数y=$\frac{1}{x+2}$与y=a|x|的图象有3个交点,
函数y=$\frac{1}{x+2}$关于(-2,0)对称,x>-2时,函数值大于0,而y=a|x|是折线,
显然x>0,a>0时,两个函数一定有一个交点,
x<0时,y′=-$\frac{1}{({x+2)}^{2}}$,设切点(m,n),
则:-$\frac{1}{(m+2)^{2}}=\frac{\frac{1}{m+2}}{m}$,解得m=-1,所以a=1时,
函数y=$\frac{1}{x+2}$与y=-ax相切,函数(x<0)有两个交点,必须a>1,
综上,a>1时,关于x的方程$\frac{1}{x+2}=a|x|$有三个不同的实数解,
故选:C.
点评 本题考查函数的导数以及函数的零点判定定理的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
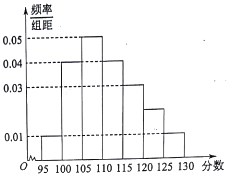 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6≤k≤2 | B. | -6≤k≤-2 | C. | -2≤k≤6 | D. | 2≤k≤6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<t<\frac{1}{2e}$ | B. | $\frac{1}{2e}<t<\frac{1}{2}$ | C. | $\frac{1}{2}<t<\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}<t<\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com