
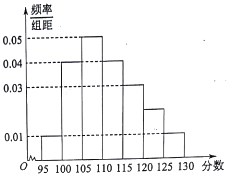
 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.分析 (1)先求出分数在110-120内的学生的频率,由此能求出该班总人数,再求出分数在120-125内的学生的频率,由此能求出分数在120-125内的人数.
(2)利用频率分布直方图,能估算该班学生数学成绩的众数和中位数.
(3)由题意分数在115-120内有学生6名,其中男生有2名.设女生为A1,A2,A3,A4,男生为B1,B2,从6名学生中选出2名,利用列举法能求出其中至多含有1名男生的概率.
解答 解:(1)分数在110-120内的学生的频率为P1=(0.04+0.03)×5=0.35,
所以该班总人数为$N=\frac{14}{0.35}=40$.
分数在120-125内的学生的频率为:P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.10,
分数在120-125内的人数为n=40×0.10=4.
(2)由频率直方图可知众数是最高的小矩形底边中点的横坐标,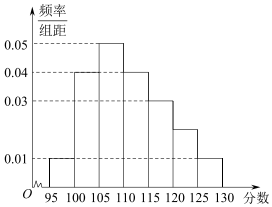
即为$\frac{105+110}{2}=107.5$.
设中位数为a,∵0.01×5+0.04×5+0.05×5=0.50,∴a=110.
∴众数和中位数分别是107.5,110.
(3)由题意分数在115-120内有学生40×(0.03×5)=6名,其中男生有2名.
设女生为A1,A2,A3,A4,男生为B1,B2,从6名学生中选出2名的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),
(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A3,B1),(A4,B1),
(A3,B1),(A4,B2),(A3,B1),(B1,B2),共15种,
其中至多有1名男生的基本事件共14种,
∴其中至多含有1名男生的概率为$P=\frac{14}{15}$.
点评 本题考查古典概型及应用,考查概率的计算,考查计数原理,考查排列组合,解答本题的关键是正确理解获奖的情形,解题时要要认真审题,注意排列组合公式的合理运用,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [$\frac{1}{2},1$] | C. | ($\frac{1}{2},1$) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥中P-ABCD,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=$\sqrt{2}$,BC=2$\sqrt{2}$,PA=2.
如图,在四棱锥中P-ABCD,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=$\sqrt{2}$,BC=2$\sqrt{2}$,PA=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com