
分析 (1)通过讨论a的范围,求出函数f(x)的最小值,得到关于a的方程,解出即可;
(2)求出m+n=6,根据不等式的性质求出m2+n2的最小值即可.
解答 解:(1)①当$-1>-\frac{a}{2}$时,即a>2时,
$f(x)=\left\{\begin{array}{l}-3x-(1+a),x≤-\frac{a}{2}\\ x+a-1,-\frac{a}{2}<x<-1\\ 3x+(a+1),x≥-1\end{array}\right.$,
则当$x=-\frac{a}{2}$时,$f{(x)_{min}}=f(-\frac{a}{2})=|{-\frac{a}{2}+1}|+|{-a+a}|=2$,
解得a=6或a=-2(舍);
②当$-1<-\frac{a}{2}$时,即a<2时,
$f(x)=\left\{\begin{array}{l}-3x-(1+a),x≤1\\-x+1-a,-1<x<-\frac{a}{2}\\ 3x+(a+1),x≥-\frac{a}{2}\end{array}\right.$,
则当$x=-\frac{a}{2}$时,$f{(x)_{min}}=f(-\frac{a}{2})=|{-\frac{a}{2}+1}|+|{-a+a}|=2$,
解得a=6(舍)或a=-2,
③当$-1=-\frac{a}{2}$时,即a=2,f(x)=3|x+1|,
此时f(x)min=0,不满足条件,
综上所述,a=6或a=-2;
(2)由题意知,m+n=6,
∵(m+n)2=m2+n2+2mn≤(m2+n2)+(m2+n2)=2(m2+n2)当且仅当m=n=3时取“=”,
∴m2+n2≥18,所以m2+n2的最小值为18.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
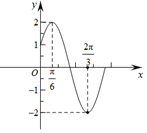 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
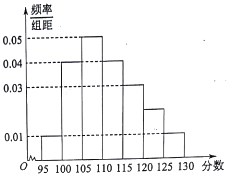 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com