
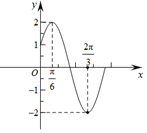
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.分析 (Ⅰ)根据图象求出A,ω 和φ,即可求函数f(x)的解析式;
(Ⅱ)由(2a-$\sqrt{3}$c)cosB=$\sqrt{3}$bcosC,利用正弦定理化简,可得B的大小,从而得到A的范围,利用三角函数的性质即可求f($\frac{A}{2}$)+sinC的取值范围.
解答 解:(Ⅰ)由图象知,A=2,T=π,∴ω=2,
由图象可知,f($\frac{π}{6}$)=2,∴2cos($\frac{π}{3}$+φ)=2,
∴$\frac{π}{3}$+φ=2kπ,又∵|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{3}$,∴f(x)=2cos(2x-$\frac{π}{3}$).
(Ⅱ)依题设(2a-$\sqrt{3}$c)cosB=$\sqrt{3}$bcosC,
∴(2sinA-$\sqrt{3}$sinC)cosB=$\sqrt{3}$sinBcosC,
即2sinAcosB=$\sqrt{3}$(sinCcosB+sinBcosC)=$\sqrt{3}$sinA,
∴cosB=$\frac{\sqrt{3}}{2}$,又B∈(0,π),∴B=$\frac{π}{6}$.∴A+C=$\frac{5π}{6}$.
由(Ⅰ)知,f($\frac{A}{2}$)+sinC=2cos(A-$\frac{π}{3}$)+sinC=3sin(A+$\frac{π}{6}$),
又∵A$∈(0,\frac{5π}{6})$,∴A+$\frac{π}{6}$∈($\frac{π}{6}$,π),∴sin(A+$\frac{π}{6}$)∈(0,1],
∴f($\frac{A}{2}$)+sinC的取值范围是(0,3].
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.


科目:高中数学 来源: 题型:选择题
| A. | 17石 | B. | 166石 | C. | 387石 | D. | 1310石 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [$\frac{1}{2},1$] | C. | ($\frac{1}{2},1$) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com