
| A. | (1,2) | B. | [$\frac{1}{2},1$] | C. | ($\frac{1}{2},1$) | D. | (2,3) |
分析 原方程化为关于m的方程-xm2+(2y-2$\sqrt{3}$)m+x-2=0,x≠0时,△<0,得(x-1)2+(y-$\sqrt{3}$)2<1,$\overrightarrow{OM}$,$\overrightarrow{ON}$夹角记作α,直线OM与圆切与M,∠xOM=30°,α∈(0o,60o),即可得出.
解答 解:原方程化为关于m的方程-xm2+(2y-2$\sqrt{3}$)m+x-2=0,x≠0时,
△<0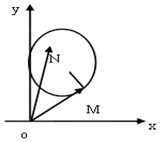 ,得(x-1)2+(y-$\sqrt{3}$)2<1,
,得(x-1)2+(y-$\sqrt{3}$)2<1,
$\overrightarrow{OM}$=($\frac{3}{2},\frac{{\sqrt{3}}}{2}$),$\overrightarrow{ON}$=(x,y),$\overrightarrow{OM}$,$\overrightarrow{ON}$夹角记作α,
直线OM与圆切与M,∠xOM=30°,α∈(0o,60o),
$\frac{{\frac{3}{2}x+\frac{{\sqrt{3}}}{2}y}}{{\sqrt{3}\sqrt{{x^2}+{y^2}}}}$=cosα∈($\frac{1}{2},1$).
故选:C.
点评 本题考查了一元二次方程的实数根与判别式的关系、直线与圆相切的性质、三角函数求值,考查了推理能力与计算能力,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [2016+$\frac{1}{ln2016}$,+∞) | B. | (2016+$\frac{1}{ln2016}$,+∞) | C. | [2016-$\frac{1}{ln2016}$,+∞) | D. | (2016-$\frac{1}{ln2016}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
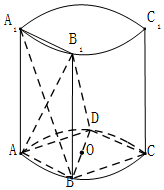 如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
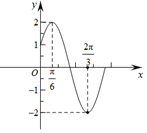 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
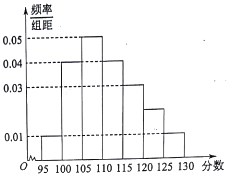 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com