
分析 (1)根据题意,设抛物线E的方程为y2=2px,由圆的方程分析可得圆心及半径,即可得$\frac{p}{2}=2$,解得p的值,代入抛物线的方程可得答案;
(2)根据题意,由等差数列的性质分析可得|AD|=|AB|+|BC|+|CD|=10,分两种情况讨论:若l垂直于x轴,分析易得此时不满足题意,若l不垂直于x轴,设l的斜率为k,可以设出l的方程为y=k(x-2),联立直线与抛物线的方程结合根与系数的关系分析可得k的值,代入直线方程中可得直线的方程,即可得答案.
解答 解:(1)根据已知设抛物线E的方程为y2=2px(p>0).
∵圆F的方程为(x-2)2+y2=1,
∴圆心F的坐标为F(2,0),半径r=1.
∴$\frac{p}{2}=2$,解得p=4.
∴抛物线E的方程为y2=8x.
(2)根据题意,∵2|BC|是|AB|与|CD|的等差中项,∴|AB|+|CD|=4|BC|=4×2r=8.
∴|AD|=|AB|+|BC|+|CD|=10.
若l垂直于x轴,则l的方程为x=2,代入y2=8x,得y=±4.
此时|AD|=|y1-y2|=8≠10,即直线x=2不满足题意.
若l不垂直于x轴,设l的斜率为k,由已知得k≠0,l的方程为y=k(x-2).
设A(x1,y1),B(x2,y2),由$\left\{{\begin{array}{l}{y=k(x-2)}\\{{y^2}=8x}\end{array}}\right.$得k2x2-(4k2+8)x+4k2=0.
∴${x_1}+{x_2}=\frac{{4{k^2}+8}}{k^2}$.
∵抛物线E的准线为x=-2,
∴|AD|=|AF|+|DF|=(x1+2)+(x2+2)=x1+x2+4,
∴$\frac{{4{k^2}+8}}{k^2}+4=10$,解得k=±2.
当k=±2时,k2x2-(4k2+8)x+4k2=0化为x2-6x+4=0,
∵△=(-6)2-4×1×4>0,∴x2-6x+4=0有两个不相等实数根.
∴k=±2满足题意,即直线y=±2(x-2)满足题意.
∴存在满足要求的直线l,它的方程为2x-y-4=0或2x+y-4=0.
点评 本题考查抛物线的几何性质,涉及直线与抛物线的位置关系,涉及直线与圆锥曲线的位置关系时,注意分析直线的斜率是否存在.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
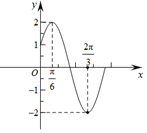 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
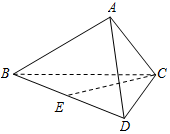 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
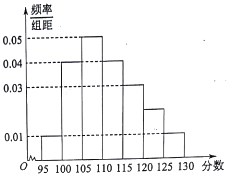 某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6≤k≤2 | B. | -6≤k≤-2 | C. | -2≤k≤6 | D. | 2≤k≤6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $2\sqrt{6}$ | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com