练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．设复数z满足$\frac{{{{（{1+i}）}^2}}}{z}=1-i$，则z=（　　）
    A．1+iB．1-iC．-1+iD．-1-i

    分析 利用复数的运算法则即可得出．

    解答 解：复数z满足$\frac{{{{（{1+i}）}^2}}}{z}=1-i$，则z=$\frac{2i}{1-i}$=$\frac{2i（1+i）}{（1-i）（1+i）}$=i-1．
    故选：C．

    点评 本题考查了复数的运算法则，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

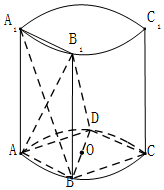    20．如图，在圆柱中，A，B，C，D是底面圆的四等分点，O是圆心，A1A，B1B，C1C与底面ABCD垂直，底面圆的直径等于圆柱的高．
    （Ⅰ）证明：BC⊥AB1；
    （Ⅱ）（ⅰ）求二面角A1-BB1-D的大小；
    （ⅱ）求异面直线AB1和BD所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．在平面直角坐标系xOy中，已知角α的顶点和点O重合，始边与x轴的非负半轴重合，终边上一点M坐标为（-1，$\sqrt{3}$），则tan（α+$\frac{π}{4}$）=$\sqrt{3}-2$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

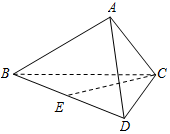    18．如图，在四面体ABCD中，平面ABC⊥平面BCD，DC⊥BC，$AB=\sqrt{3}$，BC=2，AC=1．
    （1）求证：AB⊥AD；
    （2）设E是BD的中点，若直线CE与平面ACD的夹角为30°，求四面体ABCD外接球的表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

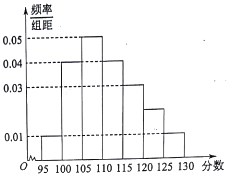    5．某校2017届高三文（1）班在一次数学测验中，全班N名学生的数学成绩的频率分布直方图如下，已知分数在110～120的学生数有14人．
    （1）求总人数N和分数在120～125的人数n；
    （2）利用频率分布直方图，估算该班学生数学成绩的众数和中位数各是多少？
    （3）现在从分数在115～120名学生（男女生比例为1：2）中任选2人，求其中至多含有1名男生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的离心率为$\frac{5}{3}$，则其渐近线方程为（　　）
    A．2x±y=0B．x±2y=0C．3x±4y=0D．4x±3y=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知向量$\overrightarrow{a}$=（5，k），$\overrightarrow{b}$=（2，-2），则使|$\overrightarrow{a}-\overrightarrow{b}$|≤5成立的充分不必要条件是（　　）
    A．-6≤k≤2B．-6≤k≤-2C．-2≤k≤6D．2≤k≤6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

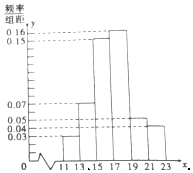    19．一企业从某生产线上随机抽取100件产品，测量这些产品的某项技术指标值x，得到的频率分布直方图如图．
    （1）估计该技术指标值x平均数$\overline x$；
    （2）在直方图的技术指标值分组中，以x落入各区间的频率作为x取该区间值的频率，若$|{x-\overline x}|＞4$，则产品不合格，现该企业每天从该生产线上随机抽取5件产品检测，记不合格产品的个数为ξ，求ξ的数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在长为16cm的线段MN上任取一点P，以MP，NP为邻边作一矩形，则该矩形的面积大于60cm2的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    同步练习册答案