
如图,在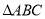 中,
中,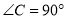 ,点
,点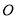 在
在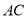 上,以
上,以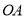 为半径的
为半径的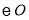 交
交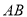 于点
于点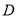 ,
,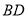 的垂直平分线交
的垂直平分线交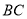 于点
于点 ,交
,交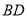 于点
于点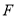 ,连接
,连接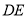 .
.
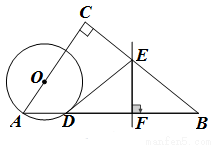
(1)判断直线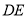 与
与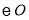 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若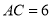 ,
,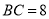 ,
, ,求线段
,求线段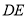 的长.
的长.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
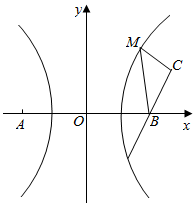 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
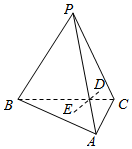 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )| A. | DE∥PB | B. | 当AB=BC且PA=AC时DE∥PB | ||
| C. | 当且仅当AB=BC且PA=AC时,DE⊥AC | D. | DE⊥AC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
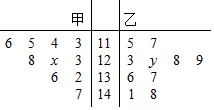 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com