
分析 (1)由二次函数的性质可知,当n=k时,Sn=-$\frac{1}{2}$n2+kn取得最大值,代入可求k,然后利用an=sn-sn-1可求通项
(2)根据已知条件推知bm=(4m+$\frac{9}{2}$)-(2m+$\frac{9}{2}$)=4m-2m,则结合(1)中的通项公式和已知条件cm=$\frac{{a}_{m}•{b}_{m}}{{2}^{m}}$得出:cm=($\frac{9}{2}$-m)×2m-($\frac{9}{2}$-m),然后利用分组求和法来求数列{cn}的前m项和Tm.
解答 解:(1)∵Sn=-$\frac{1}{2}$n2+kn=-$\frac{1}{2}$(n-k)2+$\frac{{k}^{2}}{2}$,
∴当n=k时,(Sn)max=$\frac{{k}^{2}}{2}$=8,
解得k=4,
∴Sn=-$\frac{1}{2}$n2+4n,
当n=1时,a1=S1=$\frac{7}{2}$,
当n≥2时,an=sn-sn-1=$\frac{9}{2}$-n,
显然a1=$\frac{7}{2}$适合an=$\frac{9}{2}$-n,
∴数列{an}的通项公式为an=$\frac{9}{2}$-n(n∈Z+);
(2)依题意有-4m<$\frac{9}{2}$-n<-2m,则2m+$\frac{9}{2}$<n<4m+$\frac{9}{2}$,
又m∈Z+,
∴bm=(4m+$\frac{9}{2}$)-(2m+$\frac{9}{2}$)=4m-2m,
∴cm=$\frac{{a}_{m}•{b}_{m}}{{2}^{m}}$=$\frac{(\frac{9}{2}-m)({4}^{m}-{2}^{m})}{{2}^{m}}$=($\frac{9}{2}$-m)×2m-($\frac{9}{2}$-m),且am=$\frac{9}{2}$-m,前m项和为:Am=$\frac{m(\frac{7}{2}+\frac{9}{2}-m)}{2}$=$\frac{-{m}^{2}+8m}{2}$;
令tm=($\frac{9}{2}$-m)×2m,前m和为记为:Bm,
则Bm=$\frac{7}{2}$×2+$\frac{5}{2}$×22+$\frac{3}{2}$×23+$\frac{1}{2}$×24+…+($\frac{9}{2}$-m)×2m,①
∴2Bm=$\frac{7}{2}$×22+$\frac{5}{2}$×23+$\frac{3}{2}$×24+$\frac{1}{2}$×25+…+($\frac{9}{2}$-m)×2m+1,②
∴由①-②得:-Bm=$\frac{7}{2}$×2-(22+23+24+…+2m)-($\frac{9}{2}$-m)×2m+1=7-$\frac{4-{2}^{m+1}}{1-2}$-($\frac{9}{2}$-m)×2m+1=11-(11-2m)×2m,
∴Bm=(11-2m)×2m-11
∴Tm=Bm-Am=(11-2m)×2m-11-$\frac{-{m}^{2}+8m}{2}$=(11-2m)×2m+$\frac{{m}^{2}-8m-22}{2}$.
点评 本题主要考查了等差数列的性质及通项公式的应用,等比数列的求和公式的应用,属于等差数列与等比数列基本运算的综合应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
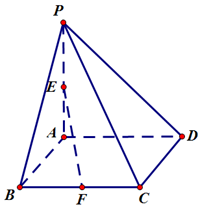 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},1)$ | C. | (1,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com