Question

13．已知函数f（x）=log_ax+x-3（a＞0且a≠1）有两个零点x₁，x₂，且x₁＜x₂，若x₂∈（3，4），则实数a的取值范围是（　　）

• A． $（0，\frac{1}{4}）$
• B． $（\frac{1}{4}，1）$
• C． （1，4）
• D． （4，+∞）

Answer 1

分析 函数f（x）有两个不同的零点，可转化为函数y=log_ax与y=3-x的图象有两个交点，在同一坐标系中，分别作出这两个函数的图象，观察图象，可得答案．

解答 解：若函数f（x）有两个不同的零点，
则函数y=log_ax与y=3-x的图象有两个交点，
在同一坐标系中，分别作出这两个函数的图象，如下图所示：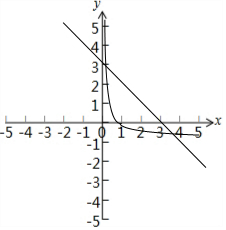

观察图象，可知若使二者有两个交点，须使0＜a＜1；
而若使x₂∈（3，4），又须使$\left\{{\begin{array}{l}{{{log}_a}3＜0}\\{{{log}_a}4＞-1}\end{array}}\right.$
解得$0＜a＜\frac{1}{4}$．
故选：A

点评 本题主要考查了函数的零点和图象的交点的关系，以及对数函数的性质，难度中档．