
分析 构造函数,利用导数求出函数的最值,再分类讨论即可求出答案.
解答 解:f(x)=$\frac{2}{x}$-ax+b,
∴f′(x)=-$\frac{2}{{x}^{2}}$-a,
∵a>0,
∴f′(x)=-
| 2 |
| x2 |
点评 本题考查了函数存在性的问题,关键是构造函数判断函数的最值,属于中档题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
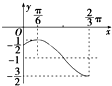 如图是函数y=Asin(ωx+ϕ)+b,(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的一段图象.求此函数解析式,并求出对称轴方程.
如图是函数y=Asin(ωx+ϕ)+b,(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的一段图象.求此函数解析式,并求出对称轴方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y | B. | x<y | C. | x=y | D. | 与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | ¬(p∨q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
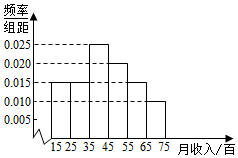 2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com