
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若方程![]() 有两个实数根,求实数
有两个实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2) ![]()
【解析】
(1)由题意,求得函数的导数,分类讨论,即可求解函数的单调区间;
(2)令![]() ,知
,知![]() 单调递增且有大于0的零点,不妨设为
单调递增且有大于0的零点,不妨设为![]() ,若有
,若有![]() 有两个零点,需满足
有两个零点,需满足![]() ,即
,即![]() ,令
,令![]() ,
,
得出![]() 在
在![]() 上单调递减,求得
上单调递减,求得![]() 的解集为
的解集为![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,进而利用函数的单调性求解.
,进而利用函数的单调性求解.
(1)由题可得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
(2)令![]() ,
,![]() ,易知
,易知![]() 单调递增且一定有大于0的零点,不妨设为
单调递增且一定有大于0的零点,不妨设为![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
故若有![]() 有两个零点,需满足
有两个零点,需满足![]() ,
,
即![]()
![]() ,
,
令![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,所以
,所以![]() 的解集为
的解集为![]() ,
,
由![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,
,
有![]() ,
,
令![]() ,
,
由于![]() ,所以
,所以![]() ,
,![]() ,
,
故![]() ,所以
,所以![]() ,
,
故![]() ,
,![]() 在
在![]() 上有唯一零点,另一方面,在
上有唯一零点,另一方面,在![]() 上,
上,
当![]() 时,由
时,由![]() 增长速度大,所以有
增长速度大,所以有![]() ,
,
综上,![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:
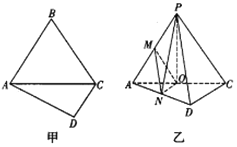
【题目】如图所示甲,在四边形ABCD中,![]() ,
,![]() ,
,![]() 是边长为8的正三角形,把
是边长为8的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
![]() 求证:
求证:![]() 平面PON;
平面PON;
![]() 求三棱锥
求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当a=1时,写出![]() 的单调递增区间(不需写出推证过程);
的单调递增区间(不需写出推证过程);
(Ⅱ)当x>0时,若直线y=4与函数![]() 的图像交于A,B两点,记
的图像交于A,B两点,记![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)若关于x的方程![]() 在区间(1,2)上有两个不同的实数根,求实数a的取值范围.
在区间(1,2)上有两个不同的实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学中仅有一人申请了北京大学的自主招生考试,当他们被问到谁申请了北京大学的自主招生考试时,甲说:“丙或丁申请了”;乙说:“丙申请了”;丙说:“甲和丁都没有申请”;丁说:“乙申请了”,如果这四位同学中只有两人说的是对的,那么申请了北京大学的自主招生考试的同学是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学中仅有一人申请了北京大学的自主招生考试,当他们被问到谁申请了北京大学的自主招生考试时,甲说:“丙或丁申请了”;乙说:“丙申请了”;丙说:“甲和丁都没有申请”;丁说:“乙申请了”,如果这四位同学中只有两人说的是对的,那么申请了北京大学的自主招生考试的同学是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com