练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．把4名学生分到3个不同的小组里去，每个小组至少一人，共有36种不同分配．

    分析 根据题意四名学生中有两名学生分在一个小组有C42种，再分到三个不同的小组有A33种，进而再利用分步计数原理计算出答案

    解答 解：由题意，四名学生中有两名学生分在一个小组有C42种，再分到三个不同的小组有A33种，
    故4名学生分到3个不同的小组里去，每个小组至少一人，共有C42A33=36种不同的分配方法．
    故答案为：36．

    点评 本题主要考查了分配问题，解决此类问题的关键是熟练掌握分步计数原理与分步计数原理，以及能够观察出4名学生的分配方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．点P是曲线y=x2-lnx上任意一点，则点P到直线x-y+2=0的最短距离为（　　）
    A．$\sqrt{3}$B．$\frac{{3\sqrt{3}}}{2}$C．$\frac{{2\sqrt{2}}}{3}$D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．为了解春季昼夜温差大小与某种子发芽多少之间的关系，现在4月份的30天都记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，从中随机挑选了5天进行分析研究，得到如表格：
    日期4月1日4月7日4月15日4月21日4月30日
    温差x/℃101113128
    发芽数y/颗2325302616
    （1）请根据4月7日、15日和21日的三天数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
    （2）若某天种子发芽率不低于$\frac{1}{4}$，则称该天种子发芽情况为“长势喜人”．根据表中5天的数据，以频率为概率，估计4月份的整体种子发芽情况．若在4月份中随机挑选3天，记“长势喜人”的天数为X，求X的分布列及数学期望．（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．某公司为了了解用电量y（单位：度）与气温x（单位：℃）之间的关系，随机统计了某4天的用电量与当天气温，数据如表：
    气温（℃）141286
    用电量22263438
    （1）由散点图知，用电量y与气温x具有线性相关关系，求y关于x的线性回归方程；
    （2）根据（1）所求的线性回归方程估计气温为10℃时的用电量．
    参考公式：b=$\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，a=$\overline{y}$-b$\overline{x}$；$\sum_{i=1}^{4}$xiyi=1120，$\sum_{i=1}^{4}$xi2=440．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（0，1），且离心率为$\frac{\sqrt{2}}{2}$．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）若直线l：y=k（x-1）+1与椭圆E交于不同两点M，N，线段MN的中点为P，O为坐标原点，且直线OP的斜率存在，求直线l与直线PO的斜率之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．掷一个六面体的骰子，点数6，5向上的概率等于$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．4个不同的小球放入编号为1、2、3、4的四个盒子中，恰有一个空盒子的概率为$\frac{9}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．现有三本相同的语文书和一本数学书，分发给三个学生，每个学生至少分得一本，问这样的分法有（　　）种．
    A．36B．9C．18D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

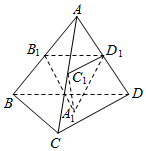    13．如图，在四面体ABCD中，点B1，C1，D1分别在棱AB，AC，AD上，且平面B1C1D1∥平面BCD，A1为△BCD内一点，记三棱锥A1-B1C1D1的体积为V，设$\frac{{A{D_1}}}{AD}=x$，对于函数V=F（x），则下列选项正确的是（　　）
    A．函数F（x）在$（{\frac{1}{2}，1}）$上是减函数
    B．函数F（x）的图象关于直线$x=\frac{1}{2}$对称
    C．当$x=\frac{2}{3}$时，函数F（x）取得最大值
    D．存在x0，使得$F（{x_0}）＞\frac{7}{27}{V_{A-BCD}}$（其中VA-BCD为四面体ABCD的体积）

    查看答案和解析>>

    同步练习册答案