
分析 利用先分组,后排列的方法求恰好有一个盒子空的放法种数,再求出4个不同的小球球随机的放入编号为1、2、3、4的四个盒子的放法种数,代入古典概型概率公式计算.
解答 解:每个小球都有4种放法,故共有44=256种不同的放法,
四个不同的小球放入编号为1,2,3,4的四个盒子中,恰有一个空盒,说明恰有一个盒子中有2个小球,
从4个小球中选两个作为一个元素,同另外两个元素在三个位置全排列,故共有C42A43=144种不同的放法,
故4个不同的小球放入编号为1、2、3、4的四个盒子中,恰有一个空盒子的概率为$\frac{144}{256}$=$\frac{9}{16}$,
故答案为:$\frac{9}{16}$
点评 本题考查了古典概型的概率计算,考查了排列组合的应用,本题采用了先分组,后排列的方法求恰好有一个盒子空的放法种数.


科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
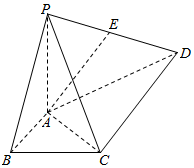 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2006 | B. | 4008 | C. | 4012 | D. | 2008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com