
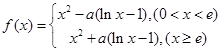 ,其中
,其中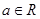 .
.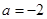 时,求函数
时,求函数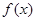 在区间
在区间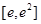 上的最大值;
上的最大值;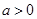 时,若
时,若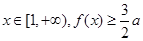 恒成立,求
恒成立,求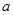 的取值范围.
的取值范围.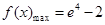 ;(2)
;(2)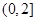 .
.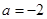 时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数
时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数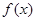 是分段函数,所以根据函数定义域把所求区间从
是分段函数,所以根据函数定义域把所求区间从 断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.
断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.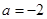 ,
,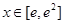 时,
时,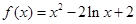 ,
,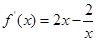 ,∴当
,∴当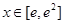 时,
时,  ,
,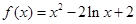 在
在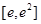 上单调递增,
上单调递增, .(4分)
.(4分)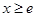 时,
时, ,
, ,
,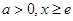 ,∴
,∴ ,∴
,∴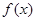 在
在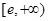 上为增函数,
上为增函数,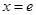 时,
时, ;
; 时,
时, ,
,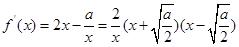 ,
,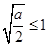 即
即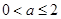 时,
时,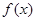 在区间
在区间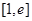 上为增函数,
上为增函数, 时,
时,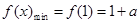 ,且此时
,且此时 ;
; ,即
,即 时,
时,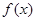 在区间
在区间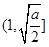 上为减函数,在区间
上为减函数,在区间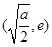 上为增函数,
上为增函数,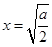 时,
时,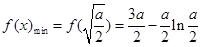 ,且此时
,且此时 ;
; ,即
,即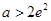 时,
时, 在区间
在区间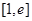 上为减函数,
上为减函数,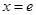 时,
时, .
.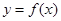 在
在 上的最小值为
上的最小值为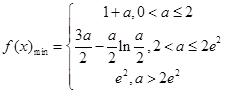
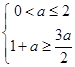 ,得
,得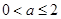 ;由
;由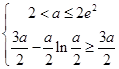 ,得无解;
,得无解;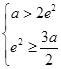 ,得无解;
,得无解;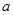 的取值范围是
的取值范围是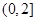 .(12分)
.(12分)

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:不详 题型:单选题
 >f(x),则 ( )
>f(x),则 ( )A.f(2)< f(0) f(0) | B.f(2)≤ f(0) f(0) |
C.f(2)= f(0) f(0) | D.f(2)> f(0) f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com