
| A. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | B. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{1}{3}})^5}$ | C. | $C_7^3×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | D. | $C_7^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^5}$ |
分析 S7=3说明共摸球七次,只有两次摸到红球,由于每次摸球的结果数之间没有影响,故可以用独立事件的概率乘法公式求解.
解答 解:由题意S7=3说明共摸球七次,只有两次摸到红球,其余的5次摸到白球,
因为每次摸球的结果数之间没有影响,摸到红球的概率是$\frac{2}{3}$,摸到白球的概率是$\frac{1}{3}$,
所以只有两次摸到红球的概率是${C}_{7}^{2}$•${(\frac{2}{3})}^{2}$•${(\frac{1}{3})}^{5}$,
故选:D.
点评 本题考查独立事件的概率乘法公式,考查学生分析解决问题的能力,确定S7=3说明共摸球七次,只有两次摸到红球,是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
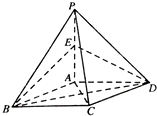 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
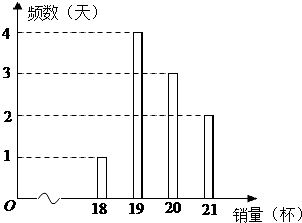 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.
如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com