
| A. | (0,$\frac{\sqrt{5}-1}{2}$)∪($\frac{\sqrt{5}+1}{2}$,+∞) | B. | ($\frac{\sqrt{5}-1}{2}$,1)∪(1,$\frac{\sqrt{5}+1}{2}$) | C. | (0,$\frac{\sqrt{3}-1}{2}$)∪($\frac{\sqrt{3}+1}{2}$,+∞) | D. | ($\frac{\sqrt{3}-1}{2}$,1)∪(1,$\frac{\sqrt{3}+1}{2}$) |
分析 根据题意,得出an、bn的解析式,讨论a>1和0<a<1时,满足的条件,从而求出a的取值范围.
解答 解:由题意得,点Bn(n,0),An(an,bn)满足|AnBn|=|AnBn+1|,
由中点坐标公式,可得BnBn+1的中点为(n+$\frac{1}{2}$,0),
即an=n+$\frac{1}{2}$,bn=${a}^{n+\frac{1}{2}}$;
当a>1时,以bn-1,bn,bn+1为边长能构成一个三角形,
只需bn-1+bn+1>bn,
bn-1<bn<bn+1,
即${a}^{n-\frac{1}{2}}$+${a}^{n+\frac{3}{2}}$>${a}^{n+\frac{1}{2}}$,
即有1+a2<a,
解得1<a<$\frac{1+\sqrt{5}}{2}$;
同理,0<a<1时,解得$\frac{\sqrt{5}-1}{2}$<a<1;
综上,a的取值范围是1<a<$\frac{1+\sqrt{5}}{2}$或$\frac{\sqrt{5}-1}{2}$<a<1,
故选:B.
点评 本题考查了指数函数的图象与性质的应用问题,也考查了数列递推公式的应用问题,考查了分类讨论思想的应用问题,是综合性题目.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
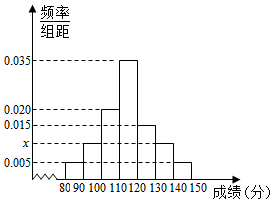 40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:
40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (1,2] | C. | $(\frac{1}{2},\frac{7}{2})$ | D. | 以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 甲 | 5 | 10 | 34 | 11 |
| 乙 | 8 | 12 | 31 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 复数的模总是正实数 | |
| B. | 复数集与复平面内所有向量组成的集合一一对应 | |
| C. | 如果与复数z对应的点在第一象限,则与该复数对应的向量的终点也一定会在第一象限 | |
| D. | 相等的向量对应着相等的复数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+$\sqrt{2}$ | B. | 4-$\sqrt{2}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | 1 | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com