
(本题满分14分)如图,四棱锥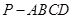 的底面
的底面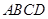 为矩形,且
为矩形,且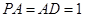 ,
,
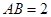 ,
,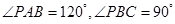 ,
,

(Ⅰ)平面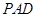 与平面
与平面 是否垂直?并说明理由;
是否垂直?并说明理由;
(Ⅱ)求直线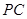 与平面
与平面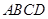 所成角的正弦值.
所成角的正弦值.
(I)见解析;(Ⅱ)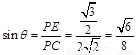 .
.
【解析】本试题主要是考查了面面垂直和线面角的求解的综合运用。
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。

(I)平面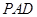
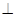 平面
平面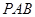 ; …………………1分
; …………………1分
证明:由题意得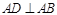 且
且
又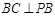 ,则
,则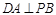 …………………………3分
…………………………3分
则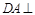 平面
平面 ,
………………5分
,
………………5分
故平面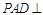 平面
平面 ………………7分
………………7分
(Ⅱ)解法1:以点A为坐标原点,AB所在的直线为y轴建立
空间直角坐标系如右图示,则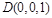 ,
,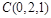 ,
, 可得
可得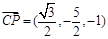 , 9分
, 9分
平面ABCD的单位法向量为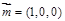 , ……………………………………11分
, ……………………………………11分
设直线PC与平面ABCD所成角为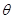 ,则
,则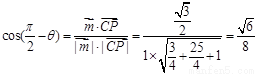 13分
13分
则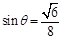 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值 ……………………………14分
……………………………14分
解法2:

由(I)知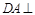 平面
平面 ,∵
,∵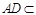 面
面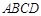
∴平面ABCD⊥平面PAB, …………………………9分
在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,
则∠PCE为直线PC与平面ABCD所成的角, …………………………11分
在Rt△PEA中,∵∠PAE=60°,PA=1,∴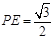 ,
,
又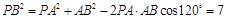
∴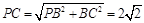 …………………………13分
…………………………13分
在Rt△PEC中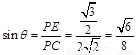 .………………14分
.………………14分


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
(本题满分14分)如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图,已知直三棱柱ABC—A1B1C1,![]() ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,![]()
(1)求证:![]() ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.

(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
(本题满分14分)如图,正方形 、
、 的边长都是1,平面
的边长都是1,平面
 平面
平面 ,点
,点 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)

(I)求 的长;
的长;
(II) 为何值时,
为何值时, 的长最小;
的长最小;
(III)当 的长最小时,求面
的长最小时,求面 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
查看答案和解析>>
科目:高中数学 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分14分)如图,矩形BCC1B1所在平面垂直于三角形ABC所在平面,BB1=CC1=AC=2, ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。
 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com