
【题目】已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线![]() 对称.
对称.
(1)求双曲线C的方程;
(2)设直线![]() 与双曲线C的左支交于A、B两点,另一直线
与双曲线C的左支交于A、B两点,另一直线![]() 经过
经过![]() 及AB的中点,求直线
及AB的中点,求直线![]() 在y轴上的截距b的取值范围;
在y轴上的截距b的取值范围;
(3)若Q是双曲线C上的任一点,![]() 、
、![]() 为双曲线C的左、右两个焦点,从
为双曲线C的左、右两个焦点,从![]() 引
引![]() 的角平分线的垂线,垂足为N,试求点N的轨迹方程.
的角平分线的垂线,垂足为N,试求点N的轨迹方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)设双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,则
,则![]() ,由该直线与圆
,由该直线与圆![]() 相切,知双曲线
相切,知双曲线![]() 的两条渐近线方程为
的两条渐近线方程为![]() .由此利用双曲线
.由此利用双曲线![]() 的一个焦点为
的一个焦点为![]() ,能求出双曲线
,能求出双曲线![]() 的方程.
的方程.
(2)由![]() ,得
,得![]() .令
.令![]() .直线与双曲线左支交于两点,等价于方程
.直线与双曲线左支交于两点,等价于方程![]() 在
在![]() 上有两个不等实根.由此能求出直线
上有两个不等实根.由此能求出直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围.
的取值范围.
(3)若![]() 在双曲线的右支上,则延长
在双曲线的右支上,则延长![]() 到
到![]() ,使
,使![]() ,若
,若![]() 在双曲线的左支上,则在
在双曲线的左支上,则在![]() 上取一点
上取一点![]() ,使
,使![]() .由此能求出点
.由此能求出点![]() 的轨迹方程.
的轨迹方程.
(1)设双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,则
,则![]() ,
,
![]() 该直线与圆
该直线与圆![]() 相切,
相切,
![]() 双曲线
双曲线![]() 的两条渐近线方程为
的两条渐近线方程为![]() .
.
故设双曲线![]() 的方程为
的方程为![]() .
.
又双曲线![]() 的一个焦点为
的一个焦点为![]() ,
,
![]() ,
,![]() .
.
![]() 双曲线
双曲线![]() 的方程为
的方程为![]() .
.
(2)由![]() ,得
,得![]() .
.
令![]()
直线与双曲线左支交于两点,等价于方程![]() 在
在![]() 上有两个不等实根.
上有两个不等实根.
因此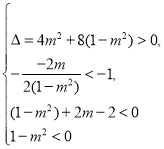 ,解得
,解得![]() .
.
又![]() 中点为
中点为![]() ,
,
因为直线![]() 与
与![]() 轴相交,所以
轴相交,所以![]() ,即
,即![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得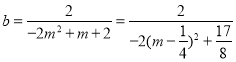 .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
(3)若![]() 在双曲线的右支上,
在双曲线的右支上,
则延长![]() 到
到![]() ,使
,使![]() ,
,
若![]() 在双曲线的左支上,
在双曲线的左支上,
则在![]() 上取一点
上取一点![]() ,使
,使![]() .
.
根据双曲线的定义![]() ,
,
所以点![]() 在以
在以![]() 为圆心,2为半径的圆上,
为圆心,2为半径的圆上,
即点![]() 的轨迹方程是
的轨迹方程是![]() ①
①
由于点![]() 是线段
是线段![]() 的中点,
的中点,
设![]() ,
,![]() ,
,![]() .
.
则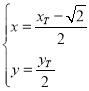 ,即
,即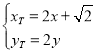 .
.
代入①并整理得点![]() 的轨迹方程为
的轨迹方程为![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.
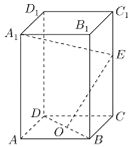
(1)证明:BD⊥A1E;
(2)如果AB=2,![]() ,OE⊥A1E,求AA1的长.
,OE⊥A1E,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率![]() ;
;
(2)根据统计数据估计图书分类错误的概率![]() ;
;
(3)假设文学类图书在“文学类专栏”、“科普类专栏”、“其他类专栏”的数目分别为![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,![]() 的方差
的方差![]() 最大时,求
最大时,求![]() ,
,![]() 的值,并求出此时方差
的值,并求出此时方差![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,
的图象,![]() 图象关于原点对称;②向量
图象关于原点对称;②向量![]() ,
,![]() ;③函数
;③函数![]()
![]() 这三个条件中任选一个,补充在下面问题中,并解答.已知_________,函数
这三个条件中任选一个,补充在下面问题中,并解答.已知_________,函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() 且
且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() 且满足:
且满足:![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 求
求![]() 的值;
的值;
(3)是否存在大于2的正整数![]() 使得
使得![]() ?若存在,求出所有符合条件的
?若存在,求出所有符合条件的![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ).
).
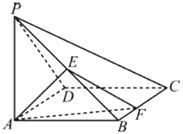
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果是,请证明;如果不是,请说明理由;
是否互相垂直?如果是,请证明;如果不是,请说明理由;
(2)求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数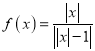 ,给出以下四个命题:(1)当
,给出以下四个命题:(1)当![]() 时,
时,![]() 单调递减且没有最值;(2)方程
单调递减且没有最值;(2)方程![]() 一定有实数解;(3)如果方程
一定有实数解;(3)如果方程![]() (
(![]() 为常数)有解,则解得个数一定是偶数;(4)
为常数)有解,则解得个数一定是偶数;(4)![]() 是偶函数且有最小值.其中假命题的序号是____________.
是偶函数且有最小值.其中假命题的序号是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com