
| A. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | B. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | D. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) |
分析 由若f(x)≤|f($\frac{π}{6}$)|对x∈R恒成立,结合函数最值的定义,求得f($\frac{π}{6}$)等于函数的最大值或最小值,由此可以确定满足条件的初相角φ的值,再根据余弦型函数单调区间的求法,即可得到答案.
解答 解:若f(x)≤|f($\frac{π}{6}$)|对x∈R恒成立,
则f($\frac{π}{6}$)等于函数的最大值或最小值,
即2×$\frac{π}{6}$+φ=kπ,k∈Z,
则φ=kπ-$\frac{π}{3}$,k∈Z,
又0<φ<π,
所以φ=$\frac{2π}{3}$,
所以f(x)=cos(2x+$\frac{2π}{3}$);
令2x+$\frac{2π}{3}$∈[2kπ,2kπ+π],k∈Z,
解得x∈[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z);
则f(x)的单调递减区间是[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z).
故选:D.
点评 本题主要考查了余弦型函数的图象与性质的应用问题,其中解题的关键是根据已知条件求出满足条件的初相角φ的值,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
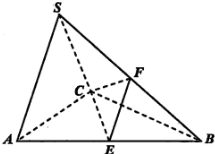 在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,$SA=SC=\sqrt{3}$,E,F分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,$SA=SC=\sqrt{3}$,E,F分别为AB,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $λ>-\frac{1}{2}$ | B. | $λ<-\frac{1}{2}$ | C. | λ>-$\frac{1}{2}$且λ≠2 | D. | λ<-$\frac{1}{2}$且λ≠2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com