
如图,已知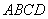 为平行四边形,
为平行四边形,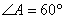 ,
,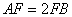 ,
,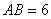 ,点
,点 在
在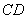 上,
上,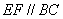 ,
,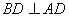 ,
,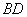 与
与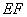 相交于
相交于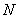 .现将四边形
.现将四边形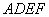 沿
沿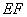 折起,使点
折起,使点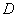 在平面
在平面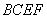 上的射影恰在直线
上的射影恰在直线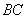 上.
上.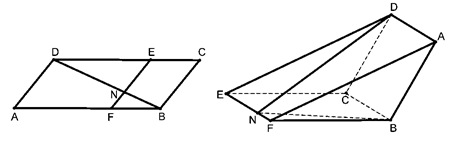
(Ⅰ) 求证: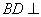 平面
平面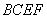 ;
;
(Ⅱ) 求折后直线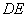 与平面
与平面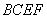 所成角的余弦值.
所成角的余弦值.
(1)要证明线面垂直,只要通过线线垂直来判定线面垂直即可。
(2)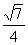
解析试题分析:解:(Ⅰ)∵EF⊥DN,EF⊥BN,DN∩BN=N
∴EF⊥面DNB ∵EF?平面BCEF,∴平面BDN⊥平面BCEF,∵BN=平面BDN∩平面BCEF,∴D在平面BCEF上的射影在直线BN上,∵D在平面BCEF上的射影在直线BC上,∴D在平面BCEF上的射影即为点B,∴BD⊥平面BCEF. 6分
(Ⅱ)连接BE,由BD⊥平面BCEF,得∠DEB即为直线DE与平面BCEF所成角.在原图中,由已知,可得AD=3,BD=3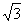 ,BN=
,BN=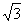 ,DN=2
,DN=2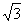 ,DE=4 折后,由BD⊥平面BCEF,知BD⊥BN则BD2=DN2-BN2=9,即BD=3则在Rt△DEB中,有BD=3,DE=4,则BE=
,DE=4 折后,由BD⊥平面BCEF,知BD⊥BN则BD2=DN2-BN2=9,即BD=3则在Rt△DEB中,有BD=3,DE=4,则BE=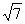 ,故cos∠DEB=
,故cos∠DEB=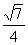 即折后直线DE与平面BCEF所成角的余弦值为
即折后直线DE与平面BCEF所成角的余弦值为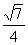 14分
14分
考点:线面垂直,线面角
点评:主要是考查了空间几何体中线面垂直的证明以及线面角的求解的综合运用,属于基础题。


科目:高中数学 来源: 题型:解答题
如图,在三棱锥A-BCD中,△ABD和△BCD是两个全等的等腰直角三角形,O为BD的中点,且AB=AD=CB=CD=2,AC=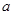 .
.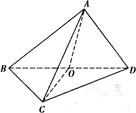
(1)当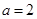 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD;
(2)当二面角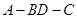 的大小为
的大小为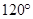 时,求二面角
时,求二面角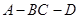 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2, CE=3,O为AB的中点.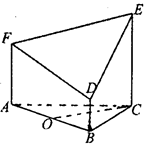
(1)求证:OC⊥DF;
(2)求平面DEF与平面ABC相交所成锐二面角的大小;
(3)求多面体ABC—FDE的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥PABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD。
(1)证明:PA⊥BD;(2)设PD=AD,求二面角A-PB-C的余弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.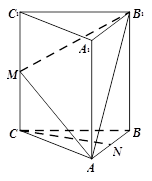
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.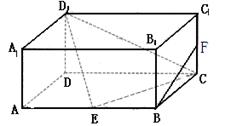
(1)证明:B F//平面E CD1
(2)求二面角D1—EC—D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com