
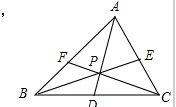
 P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24.
P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24. 分析 利用面积关系,确定$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1,即可求出xyz.
解答 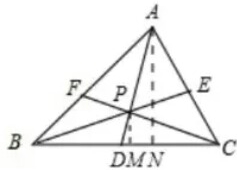 解:如图,作PM⊥BC,AN⊥BC,垂足分别为M,N,则
解:如图,作PM⊥BC,AN⊥BC,垂足分别为M,N,则
$\frac{{S}_{△PBC}}{{S}_{△ABC}}$=$\frac{x}{x+6}$,$\frac{{S}_{△PAC}}{{S}_{△ABC}}$=$\frac{y}{y+6}$,$\frac{{S}_{△PAB}}{{S}_{△ABC}}$=$\frac{z}{z+6}$,
∴$\frac{x}{x+6}$+$\frac{y}{y+6}$+$\frac{z}{z+6}$=1
∴$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1,
∴3(yz+zx+xy)+36(x+y+z)+324=xyz+6(xy+yz+zx)+36(x+y+z)+216,
∵xy+yz+zx=28,
∴xyz=108-3(xy+yz+zx)=24.
故答案为:24.
点评 本题考查三角形面积的计算,考查学生分析解决问题的能力,确定$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1是关键.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=$\frac{x}{x}$ | B. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com