考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取CD1中点G,连结FG,由已知推导出四边形FGEB为平行四边形,由此能证明BF∥平面ECD1.
(2)连结DE,E为AB的中点,DE⊥EC,DD1⊥EC,由已知得∠DED1为二面角D1-EC-D的平面角,由此能求出二面角D1-EC-D的余弦值.
解答:
(1)证明:取CD
1中点G,连结FG.
∵F为CC
1的中点D
1,∴
FG=C1D1且FG∥C
1D
1,
∵AB=C
1D
1且AB∥C
1D
1,∴
FG=AB=BE且FG∥BE,
∴四边形FGEB为平行四边形∴BF∥GE,…(4分)
∵GE?平面ECD
1,BF?平面ECD
1,
∴BF∥平面ECD
1.…(7分)
(2)解:连结DE,
∵AD=AA
1=1,AB=2,E为AB的中点,∴DE⊥EC,…(9分)
∵DD
1⊥平面ABCD,∴DD
1⊥EC,
又DD
1∩DE=D,DD
1?平面EDD
1,
DE?平面EDD
1∴CE⊥平面EDD
1,∴CE⊥ED
1,…(11分)
∴∠DED
1为二面角D
1-EC-D的平面角.…(12分)
Rt△ADE中
DE=,
∴Rt△D
1DE中,
D1E=,
∴
cos∠DED1==.…(14分)
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

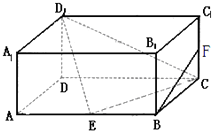 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
