
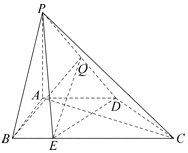
 如图,在四棱锥P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4
如图,在四棱锥P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4分析 (1)推导出DE⊥AC,PA⊥DE,由此能证明DE⊥面PAC
(2)取PD中点Q,三棱锥P-QBE体积${V}_{P-QBE}=\frac{1}{2}{V}_{P-DBE}$,由此能求出结果.
解答 证明:(1)∵在四棱锥P-ABCD,PA⊥面ABCD,AD∥BC,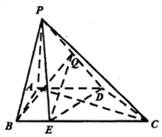
AB⊥AD,BC=2AB=2AD=2PA=4BE=4,
∴在梯形ABCD中,tan∠ADE=2=tan∠BAC,
∴∠ADE=90°-∠DAC,
∴DE⊥AC,
又∵PA⊥面ABCD,∴PA⊥DE,
∵PA∩AC=A,∴DE⊥面PAC
解:(2)取PD中点Q,
∴三棱锥P-QBE体积:
${V}_{P-QBE}=\frac{1}{2}{V}_{P-DBE}$=$\frac{1}{2}×\frac{1}{3}×{S}_{△DBE}×PA$=$\frac{1}{2}×\frac{1}{3}×\frac{1}{2}×1×2×2=\frac{1}{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
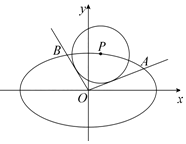 如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{4}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$均相切,且交椭圆于A,B两点.
如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{4}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$均相切,且交椭圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
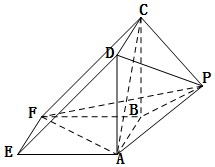 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com