
分析 (1)将A、B的坐标代入函数的解析式,求出a,b的值即可;
(2)根据函数单调性的定义证明即可;
(3)根据函数的单调性得到关于m、n的方程,求出m、n的值,从而求出m+n的值即可.
解答 解:(1)函数f(x)=$\frac{b}{x-a}$的图象过点A(0,$\frac{3}{2}$),B(3,3),
∴$\left\{\begin{array}{l}{\frac{b}{0-a}=\frac{3}{2}}\\{\frac{b}{3-a}=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$…(2分)
∴f(x)=$\frac{3}{x-2}$ …(4分)
(2)函数f(x)在(2,+∞)上单调递减,
证明:任取x2>x1>2,
则f(x1)-f(x2)=$\frac{3{(x}_{2}{-x}_{1})}{{(x}_{1}-2){(x}_{2}-2)}$…(6分)
∵x2>x1>2,
∴x2-x1>0,x1-2>0,x2-2>0,
∴$\frac{3{(x}_{2}{-x}_{1})}{{(x}_{1}-2){(x}_{2}-2)}$>0,得f(x1)-f(x2)>0,
∴f(x1)>f(x2),
函数f(x)在(2,+∞)上是单调递减函数 …(8分)
(3)∵m,n∈(2,+∞),
∴函数f(x)在[m,n]上单调递减,
∴f(m)=3,f(n)=1 …(10分)
∴$\frac{3}{m-2}$=3,$\frac{3}{n-2}$=1,
∴m=3,n=5,
∴m+n=8 …(12分)
点评 本题考查了求函数的解析式,函数的单调性以及函数的值域问题,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (2,0) | C. | (2,2) | D. | (-1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
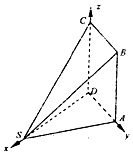 如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,$SD=\sqrt{3}AD$.
如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,$SD=\sqrt{3}AD$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
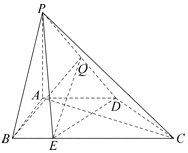 如图,在四棱锥P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4
如图,在四棱锥P-ABCD,PA⊥面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=2PA=4BE=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离.
如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com