
 如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离.
如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 分析 由∠BDC为直角,∠BCD=45°,得到三角形BCD为等腰直角三角形,可得出BD=CD=40,在三角形ACD中,利用三角形内角和定理求出∠ACD与∠CAD的度数,再由CD的长,利用正弦定理求出AD的长,在三角形ABD中,由AD,BD及cos∠ADB的值,利用余弦定理即可求出AB的长.
解答 解:∵∠BDC=90°,∠BCD=45°,
∴△BCD为等腰直角三角形,
又CD=40,
∴BD=CD=40,
在△ACD中,∠ACD=∠ACB+∠BCD=105°,∠ADC=30°,
∴∠CAD=45°,
又sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{2}+\sqrt{6}}{4}$,
由正弦定理得:AD=$\frac{40sin105°}{sin45°}$=20($\sqrt{3}$+1),
在△ABD中,利用余弦定理得:AB2=AD2+BD2-2AD•BDcos60°=400($\sqrt{3}$+1)2+402-800($\sqrt{3}$+1)=2400,
解得:AB=20$\sqrt{6}$.
点评 此题考查了正弦、余弦定理,等腰直角三角形的判定与性质,两角和与差的正弦函数公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
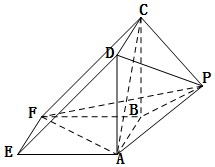 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com