
分析 (1)设点M(x,y),通过KAM•KBM=-$\frac{3}{4}$,即可求出所在的曲线C的方程.
(2)求出$P(1,\frac{3}{2})$,设直线PQ的方程,与椭圆方程联立消去y,通过x=1是方程的一个解,求出方程的另一解,求出直线RQ的斜率,把直线RQ的方程$y=\frac{1}{2}x+b$代入椭圆方程,求出|PQ原点O到直线RQ的距离,表示出面积S△OQR,求解最值.
解答 解:(1)设点M(x,y),
∵KAM•KBM=-$\frac{3}{4}$,
∴$\frac{y}{x+2}×\frac{y}{x-2}=-\frac{3}{4}$,
整理得点所在的曲线C的方程:$\frac{x^2}{4}+\frac{y^2}{3}=1\;(x≠±2)$.
(2)由题意可得点$P(1,\frac{3}{2})$,
直线PQ与直线PR的斜率互为相反数,设直线PQ的方程为$y=k(x-1)+\frac{3}{2}$,
与椭圆方程联立消去y,得:(4k2+3)x2+(12k-8k2)x+(4k2-12k-3)=0,
由于x=1是方程的一个解,
所以方程的另一解为${x_Q}=\frac{{4{k^2}-12k-3}}{{4{k^2}+3}}$,同理${x_R}=\frac{{4{k^2}+12k-3}}{{4{k^2}+3}}$,
故直线RQ的斜率为${k_{RQ}}=\frac{{{y_R}-{y_Q}}}{{{x_R}-{x_Q}}}=\frac{{-k({x_R}-1)+\frac{3}{2}-k({x_Q}-1)-\frac{3}{2}}}{{{x_R}-{x_Q}}}=\frac{{-k(\frac{{8{k^2}-6}}{{4{k^2}+3}}-2)}}{{\frac{24k}{{4{k^2}+3}}}}=\frac{1}{2}$,
把直线RQ的方程$y=\frac{1}{2}x+b$代入椭圆方程,消去y整理得x2+bx+b2-3=0,
所以|PQ|=$\sqrt{1+(\frac{1}{2})^{2}}×\frac{\sqrt{{b}^{2}-4({b}^{2}-3)}}{1}$=$\frac{\sqrt{15}}{2}×\sqrt{4-{b}^{2}}$
原点O到直线RQ的距离为$d=\frac{{\left|{2b}\right|}}{{\sqrt{5}}}$,
S△OQR=$\frac{1}{2}×\frac{\sqrt{15}}{2}×\sqrt{4-{b}^{2}}×\frac{|2b|}{\sqrt{5}}$=$\frac{\sqrt{3}}{2}\sqrt{{b}^{2}(4-{b}^{2})}$≤$\frac{\sqrt{3}}{2}•\frac{{b}^{2}+(4-{b}^{2})}{2}$=$\sqrt{3}$.
点评 本题考查直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
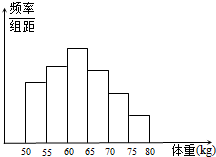 某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为236,则该校高三年级的男生总数为( )
某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为236,则该校高三年级的男生总数为( )| A. | 800 | B. | 960 | C. | 944 | D. | 888 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正三棱锥S-ABC底面边长为2$\sqrt{3}$,过侧棱SA与底面中心O作截面SAD,在△SAD中,若SA=AD,求侧面与底面所成二面角的余弦值.
已知正三棱锥S-ABC底面边长为2$\sqrt{3}$,过侧棱SA与底面中心O作截面SAD,在△SAD中,若SA=AD,求侧面与底面所成二面角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆过点$({2\sqrt{3},1})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
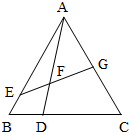 如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.
如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com