
| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 分别求出向量$\overrightarrow{AB}$、$\overrightarrow{CD}$的坐标和数量积,以及模,再由向量$\overrightarrow{AB}$在向量$\overrightarrow{CD}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{CD}|}$,计算即可得到所求值.
解答 解:由A(1,2),B(3,4),C(-2,2),D(-3,5),
可得$\overrightarrow{AB}$=(2,2),$\overrightarrow{CD}$=(-1,3),
$\overrightarrow{AB}$•$\overrightarrow{CD}$=2×(-1)+2×3=4,
|$\overrightarrow{CD}$|=$\sqrt{1+9}$=$\sqrt{10}$,
则向量$\overrightarrow{AB}$在向量$\overrightarrow{CD}$方向上的投影为:
$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{CD}|}$=$\frac{4}{\sqrt{10}}$=$\frac{2\sqrt{10}}{5}$.
故选:A.
点评 本题考查向量的投影的求法,注意运用向量的数量积的坐标表示和模的求法,考查化简整理的运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
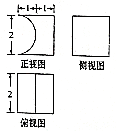 我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )| A. | 8-2π | B. | 8-π | C. | $4-\frac{π}{2}$ | D. | $8-\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,-3,-1) | B. | (-4,-3,0) | C. | (-2,-1,0) | D. | (-2,-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com