
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
分析 由题意知,Sn有最大值,所以d<0,因为$\frac{{a}_{11}}{{a}_{10}}$<-1,可得a10>0>a11,且a10+a11<0,再利用求和公式与数列的单调性即可判断出结论.
解答 解:由题意知,Sn有最大值,所以d<0,因为$\frac{{a}_{11}}{{a}_{10}}$<-1,
所以a10>0>a11,且a10+a11<0,
所以S20=10(a1+a20)=10(a10+a11)<0,则S19=19a10>0,
又a1>a2>…>a10>0>a11>a12,所以S10>S9>…>S2>S1>0,S10>S11>…>S19>0>S20>S21,
又S19-S1=a2+a3+…+a19=9(a10+a11)<0,所以S19为最小正值,
故选:C.
点评 本题考查了等差数列的通项公式与求和公式及其单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
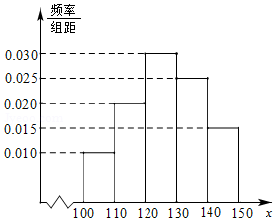 扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.
扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1$+\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 3$+\sqrt{2}$ | D. | 4$+\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com