
| A. | [$\frac{1}{2}$,$\frac{5}{4}$] | B. | [$\frac{1}{2}$,$\frac{3}{4}$] | C. | (0,$\frac{1}{2}$] | D. | (0,2] |
分析 求出f(x)的单调减区间A,令($\frac{π}{2}$,π)⊆A,解出ω的范围.
解答 解:f(x)=$\frac{\sqrt{2}}{2}$(sinωx+cosωx)=sin(ωx+$\frac{π}{4}$),
∴$\frac{π}{2}+2kπ$≤ωx+$\frac{π}{4}$≤$\frac{3π}{2}+2kπ$,函数f(x)单调递减,
$\frac{π}{4ω}+\frac{2kπ}{ω}≤x≤\frac{5π}{4ω}+\frac{2kπ}{ω}$,k∈Z,函数f(x)单调递减,
$\left\{\begin{array}{l}{\frac{π}{4ω}+\frac{2kπ}{ω}≤\frac{π}{2}}\\{\frac{5π}{4ω}+\frac{2kπ}{ω}≥π}\end{array}\right.$,解得$\frac{1}{2}$+4k≤ω≤$\frac{5}{4}$+2k,k∈Z,
故选:A.
点评 本题考查了三角函数的单调性与单调区间,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 125 | B. | 15 | C. | 100 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
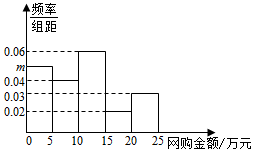 某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图
某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 6 | C. | 24 | D. | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com