
分析 (1)根据前三项系数1,$\frac{1}{2}$$c_n^1$,$\frac{1}{4}$$c_n^2$成等差数列,求得n的值,再利用二项式展开式的通项公式,求得第三项的二项式系数及项的系数.
(2)利用二项式展开式的通项公式求得含x项的系数.
解答 解:(1)∵前三项系数1,$\frac{1}{2}$$c_n^1$,$\frac{1}{4}$$c_n^2$成等差数列.
∴2•$\frac{1}{2}$$c_n^1$=1+$\frac{1}{4}$$c_n^2$,即n2-9n+8=0.∴n=8或n=1(舍).
通项公式Tr+1=$c_8^r$•($\sqrt{x}$)8-r•${(\frac{1}{2})}^{r}$•${x}^{-\frac{r}{4}}$=2-r•${C}_{8}^{r}$•${x}^{4-\frac{3r}{4}}$,r=0,1,…,8.
∴第三项的二项式系数为${C}_{8}^{2}$=28.第三项系数为 ${C}_{8}^{2}$•$\frac{1}{4}$=7.
(2)令4-$\frac{3}{4}$r=1,得r=4,∴含x项的系数为${({\frac{1}{2}})^4}$•$c_8^4$=$\frac{35}{8}$.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.


科目:高中数学 来源: 题型:解答题
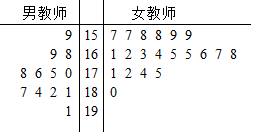 新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.
新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
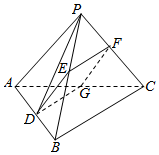 在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.
在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,$\frac{5}{4}$] | B. | [$\frac{1}{2}$,$\frac{3}{4}$] | C. | (0,$\frac{1}{2}$] | D. | (0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com